题目内容
已知函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<
)的最小值是-5,图象上相邻最高点与最低点的横坐标相差
,且图象经过点(0,
),求这个函数的解析式.
| π |
| 2 |
| π |
| 4 |
| 5 |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ,从而求得函数的解析式.
解答:
解:由题意可得,A=5,
T=
=
,∴ω=4.
再根据图象经过点(0,
),可得 5sinφ=
,sinφ=
,再结合0<φ<
可得φ=
,
故函数的解析式为f(x)=sin(4x+
).
| 1 |
| 2 |
| π |
| ω |
| π |
| 4 |
再根据图象经过点(0,
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
故函数的解析式为f(x)=sin(4x+
| π |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
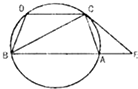 如图,已知圆上的弧
如图,已知圆上的弧
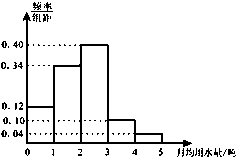 如图是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图,其中分组区间为(0,1],(1,2],(2,3],(3,4],(4,5].则由直方图可估计该城市居民月均用水量的众数是
如图是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图,其中分组区间为(0,1],(1,2],(2,3],(3,4],(4,5].则由直方图可估计该城市居民月均用水量的众数是