题目内容
执行如图所示的程序框图，则输出的结果是 ．
考点：程序框图
专题：图表型,算法和程序框图
分析：执行程序框图，依次写出每次循环得到的s，k的值，当s=48，k=9时，不满足条件s＜39，退出循环，输出k的值为9．
解答：
解：执行程序框图，有
k=1，s=0
满足条件s＜39，s=3，k=3
满足条件s＜39，s=12，k=5
满足条件s＜39，s=27，k=7
满足条件s＜39，s=48，k=9
不满足条件s＜39，退出循环，输出k的值为9．
故答案为：9．
k=1，s=0
满足条件s＜39，s=3，k=3
满足条件s＜39，s=12，k=5
满足条件s＜39，s=27，k=7
满足条件s＜39，s=48，k=9
不满足条件s＜39，退出循环，输出k的值为9．
故答案为：9．
点评：本题主要考查了程序框图和算法，属于基本知识的考查．
练习册系列答案
相关题目
已知一正方形的两顶点为双曲线C的两焦点，若另外两个项点在双曲线C上，则双曲线C的离心率e=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
极点与直角坐标系的原点重合，极轴与x轴非负半轴重合，曲线C的极坐标方程为ρ=2sinθ，直线l的参数方程为
（t为参数），直线l与曲线C交于A、B，则 线段AB的长等于（ ）
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
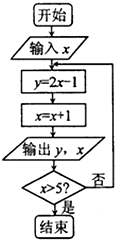如程序框图所示已知集合A={x|框图中输出的x值}，集合B={y|框图中输出的y值}，当x=1时A∩B=（ ）| A、∅ | B、{3} |
| C、{1，3，5} | D、{3，5} |
若x为实数，则函数y=x2+3x-5的最小值为（ ）
A、-
| ||
| B、-5 | ||
| C、0 | ||
| D、不存在 |
过点（
，-2）且倾斜角为120°的直线l，与圆x2+y2-2y=0的位置关系是（ ）
| 3 |
| A、相交 | B、相切 |
| C、相离 | D、位置关系不确定 |
已知函数f（x）=px2+qx+r（p≠0，p＜r），满足f（0）＜0且f（-
）＞0，设△ABC的三个内角分别为A、B、C，tanA，tanB为函数f（x）的两个零点，则△ABC一定是（ ）
| q |
| 2p |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |