题目内容
某校高二年级要排出周六上午的语文，数学，英语，物理，化学，生物6节课的课程表，要求数学课不排第一节，英语课不排第六节，不同排法种数是（ ）
| A、600 | B、504 |
| C、480 | D、288 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：根据特殊元素优先安排的原则，分两类，当英语排在第一节时，其它课任意排，第二类，当英语课不在第一节时，第一节只能从另外4课选一课，再排第六节，第六节课从包含数学四门课中任选一门，然后再排剩余的节次，问题得以解决．
解答：
解：分两类，当英语排在第一节时，其它课任意排有
=120种，当英语排在第一节时有，
=384，根据分类计数原理得不同排法种数有120+384=504．
故选B．
| A | 5 5 |
| A | 1 4 |
| •A | 1 4 |
| •A | 4 4 |
故选B．
点评：本题考查分类计数原理，特殊元素优先安排的原则，分类不重不漏，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
已知数列{an}对任意的p，q∈N*满足ap+q=ap+aq且a2=6，那么a10等于（ ）
| A、165 | B、33 | C、30 | D、21 |
若直线ax+2y+1=0与直线x+y-1=0互相垂直，那么a的值等于（ ）
| A、1 | ||
B、-
| ||
C、-
| ||
| D、-2 |
已知条件p：
≤1，条件q：x≤1，则q是￢p成立的（ ）条件．
| 1 |
| x |
| A、充分不必要 | B、必要不充分 |
| C、充要 | D、非充分非必要 |
已知p：“tanαtanβ=1”，q：“cos（α+β）=0”，那么p是q的（ ）条件．
| A、充要 |
| B、既不充分，也不必要 |
| C、必要不充分 |
| D、充分不必要 |
已知函数f（x）（x∈R）满足f（2）=3，且f′（x）＜1，则不等式f（x2）＜x2+1的解集是（ ）
A、（-∞，-
| ||||
B、（
| ||||
C、（-
| ||||
D、（-∞，-
|
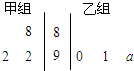如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩，乙组记录中有一个数字模糊，无法确认．假设这个数字具有随机性，并在图中以a表示．