题目内容
1.若(1+3x)100=a0+a1(x-1)+a2(x-1)2+…+a100(x-1)100,ai∈R,i=1,2,3,…,则a1+a3+a5+…+a99=$\frac{1}{2}({{7^{100}}-1})$.分析 (1+3x)100=a0+a1(x-1)+a2(x-1)2+…+a100(x-1)100,ai∈R,i=1,2,3,…,分别令x=0,x=2,相减即可得出.
解答 解:(1+3x)100=a0+a1(x-1)+a2(x-1)2+…+a100(x-1)100,ai∈R,i=1,2,3,…,
令x=0,可得:1=a0-a1+a2+…-a99+a100,
令x=2,可得:7100=a0+a1+a2+…+a99+a100,
则a1+a3+a5+…+a99=$\frac{1}{2}({7}^{100}-1)$.
故答案为:$\frac{1}{2}({7}^{100}-1)$.
点评 本题考查了二项式定理的应用、方程思想,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=x3-3x2-m存在2个零点,则这两个零点的和为( )
| A. | 1 | B. | 3 | C. | 1或4 | D. | 1或3 |
16.已知随机变量X~N(μ,σ2),则Y=aX+b服从( )
| A. | Y~N(aμ,σ2) | B. | Y~N(0,1) | C. | Y~N($\frac{μ}{a}$,$\frac{σ2}{b}$) | D. | Y~N(aμ+b,a2σ2) |
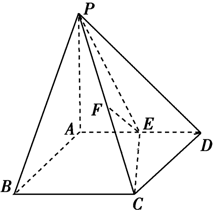 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.