题目内容
6.已知a为实数,函数f(x)=x3-ax2-4x+4a满足f′(1)=0.(1)求a的值;
(2)求f(x)的单调区间和极值;
(3)若方程f(x)=m只有一个实数根,求实数m的取值范围.
分析 (1)由原式得f(x)=x3-ax2-4x+4a,f'(x)=3x2-2ax-4.由f'(-1)=0得$a=\frac{1}{2}$,
(2)利用导数求出单调区间,再确定极值;
(3)方程f(x)=m只有一个实数根,即函数y=f(x)的图象与y=m的图象只有一个交点,利用(2)可得实数m的取值范围
解答 解:(1)由原式得f(x)=x3-ax2-4x+4a,
∴f'(x)=3x2-2ax-4.由f'(-1)=0得$a=\frac{1}{2}$,
(2)$f(x)={x^3}-\frac{1}{2}{x^2}-4x+2,f'(x)=3{x^2}-x-4$.
由f'(x)═0得$x=\frac{4}{3}$或x=-1,
| x | (-∞,-1) | -1 | $(-1,\frac{4}{3})$ | $\frac{4}{3}$ | $(\frac{4}{3},+∞)$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大 | 递减 | 极小 | 递增 |
(3)∵方程f(x)=m只有一个实数根
∴函数y=f(x)的图象与y=m的图象只有一个交点
故实数m的取值范围为$m<-\frac{50}{27}或m>\frac{9}{2}$.
点评 本题考查了导数的应用,考查了函数与方程思想、转化思想,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
14.在复平面内,复数z=i3(1+i)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.经过点P(0,2)的直线l,若直线l与连接A(-$\sqrt{3}$,-1),B(2,0)的线段总有公共点,则直线l的斜率的取值范围是( )
| A. | $[-1,\frac{{\sqrt{3}}}{3}]$ | B. | $[-1,\sqrt{3}]$ | C. | $(-∞,-1]∪[\frac{{\sqrt{3}}}{3},+∞)$ | D. | $(-∞,-1]∪[\sqrt{3},+∞)$ |
18.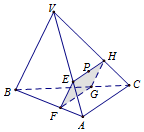 如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
 如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
15.福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
| 81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
| 06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
| A. | 12 | B. | 33 | C. | 06 | D. | 16 |
18.若直线经过A(0,3),B(0,-4)两点,则直线AB的斜率( )
| A. | 1 | B. | 0 | C. | -1 | D. | 不存在 |