题目内容
已知直线x-y+m=0与圆x2+y2=4交于不同的两点A，B，O是坐标原点．若圆周上存在一点C，使得△ABC为等边三角形，则实数m的值为 ．
考点：直线与圆的位置关系,余弦定理
专题：计算题,直线与圆
分析：先由圆心角与圆周角的关系得到∠AOB=120°，再利用余弦定理得到BD，最后借助于点到直线的距离公式可解得m即可．
解答：
解：根据题意画出图形，连接OA，OB，作OD垂直于AB于D点，
因为△ABC为等边三角形，所以∠AOB=120°，由余弦定理知：AB=2
，
故BD=
，所以OD=1，
所以O（0，0）到直线AB的距离
=1，解得m=±
，
故答案为：±
．
解：根据题意画出图形，连接OA，OB，作OD垂直于AB于D点，因为△ABC为等边三角形，所以∠AOB=120°，由余弦定理知：AB=2
| 3 |
故BD=
| 3 |
所以O（0，0）到直线AB的距离
| |m| | ||
|
| 2 |
故答案为：±
| 2 |
点评：本题考查直线与圆的位置关系，考查余弦定理，考查点到直线的距离公式，属于中档题．
练习册系列答案
相关题目
在下列关于点P，直线l、m与平面α、β的命题中，正确的是（ ）
| A、若m⊥α，l⊥m，则l∥α |
| B、若α⊥β，α∩β=m，P∈α，P∈l，且l⊥m，则l⊥β |
| C、若l，m是异面直线，m?α，m∥β，l?β，l∥α，则α∥β |
| D、若α⊥β，且l⊥β，m⊥l，则m⊥α |
数列3，7，13，21，31，…的一个通项公式是（ ）
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n（n2-1） |
函数f（x）=2-x的大致图象为（ ）
A、 |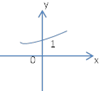
B、 |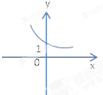
C、 |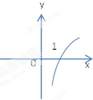
D、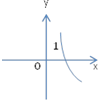 |