题目内容
8.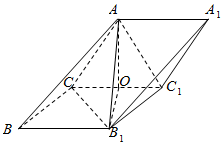 如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.(1)求证:BB1⊥AB1;
(2)若AB=2$\sqrt{3}$,求平面ABC与平面AOB1所成二面角的余弦值.
分析 (I)根据线面面垂直的判定定理证明BB1⊥平面AOB1即可
(Ⅱ)建立空间坐标系,利用向量法求出平面的法向量,利用向量法结合二面角的余弦值求出F的位置即可得到结论.
解答 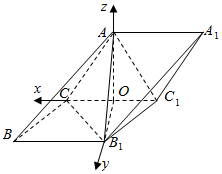 (1)证明:∵AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点,
(1)证明:∵AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点,
∴AO⊥CC1,OB1⊥CC1,
又∵AO∩OB1=O,
∴CC1⊥平面AOB1,
∵BB1∥CC1,
∴BB1⊥平面AOB1,
∵AB1?平面AOB1,
∴BB1⊥AB1;
(2)若AB=2$\sqrt{3}$,则AB1=$\sqrt{(2\sqrt{3})^{2}-(2\sqrt{2})^{2}}$=$\sqrt{4}=2$,
∵AO=B1O=$\sqrt{2}$,
∴AO2+B1O2=2+2=4=(AB1)2,
∴△AOB1是直角三角形,
则AO⊥OB1,
建立以O为坐标原点,OC,OB1,OA分别为x,y,z轴的空间直角坐标系如图:
则平面AOB1的法向量为$\overrightarrow{m}$=(1,0,0),
设平面ABC的法向量为$\overrightarrow{n}$=(x,y,z),
则A(0,0,$\sqrt{2}$),C($\sqrt{2}$,0,0),B(2$\sqrt{2}$,$\sqrt{2}$,0),
则$\overrightarrow{BC}$=(-$\sqrt{2}$,-$\sqrt{2}$,0),$\overrightarrow{AC}$=($\sqrt{2}$,0,-$\sqrt{2}$),
则$\overrightarrow{n}$•$\overrightarrow{BC}$=-$\sqrt{2}$x-$\sqrt{2}$y=0,$\overrightarrow{n}$•$\overrightarrow{AC}$=$\sqrt{2}$x-$\sqrt{2}$z=0,
则$\left\{\begin{array}{l}{x-y=0}\\{x-z=0}\end{array}\right.$,取$\overrightarrow{n}$=(1,1,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{1+1+1}}=\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$
即平面ABC与平面AOB1所成二面角的余弦值是$\frac{\sqrt{3}}{3}$.
点评 本题主要考查线面垂直的性质定理以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | 60° | B. | 30° | C. | 150° | D. | 120° |
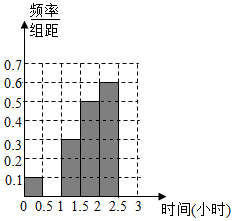 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.(1)确定x,y,p,q的值,并补全须率分布直方图;
(2)为进一步了解使用微信对自己的日不工作和生活是否有影响,从“微信达人”和“非微信达人”60人中用分层抽样的方法确定10人,若需从这10人中随积选取3人进行问卷调查,设选取的3人中“微信达人”的人数为X,求X的分布列和数学期望.
| 使用微信时间(单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |