题目内容
17.已知命题:p:关于x的方程x2+mx+1=0有两个不等的负根;q:关于x的方程4x2+4(m-2)x+1=0没有实根:若¬p或¬q为假.求实数m的取值范围.
分析 若命题p为真:则$\left\{\begin{array}{l}{△>0}\\{-m<0}\\{1>0}\end{array}\right.$;若q:关于x的方程4x2+4(m一2)x+1=0没有实根,则△<0.若¬p或¬q为假.则¬(p∧q)为假,P∧A为真,即可得出.
解答 解:命题:p:关于x的方程x2+mx+1=0有两个不等的负根,则$\left\{\begin{array}{l}{△>0}\\{-m<0}\\{1>0}\end{array}\right.$,解得m>2;
q:关于x的方程4x2+4(m一2)x+1=0没有实根,∴△=16(m-2)2-16<0,解得1<m<3.
若¬p或¬q为假.则¬(p∧q)为假,
∴p∧q为真,
由p∧q为真可得:$\left\{\begin{array}{l}{m>2}\\{1<m<3}\end{array}\right.$,解得2<m<3.
∴实数m的取值范围是:(2,3).
点评 本题考查了复合命题真假的判定方法、一元二次的实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.设抛物线C:x2=4y的焦点为F,斜率为k的直线l经过点F,若抛物线C上存在四个点到直线l的距离为2,则k的取值范围是( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | (-$\sqrt{3}$,-1)∪(1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-∞,-1)∪(1,+∞) |
2.已知平面区域D,命题P:?(x,y)∈D,x-2y+1≤0,若命题P为真命题,则平面区域D可以是( )
| A. | $\left\{\begin{array}{l}{x-y≥0}\\{x+2y≥3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y≥0}\\{x+2y≤3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-y≤0}\\{x+2y≥3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y≤0}\\{x+2y≤3}\end{array}\right.$ |
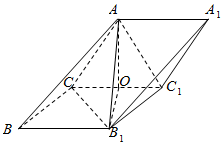 如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.