题目内容
18.化简(x-4)4+4(x-4)3+6(x-4)2+4(x-4)+1得(x-3)4.分析 由条件逆用二项式定理、二项展开式的通项公式,得出结论.
解答 解:(x-4)4+4(x-4)3+6(x-4)2+4(x-4)+1=[(x-4)+1]4=(x-3)4,
故答案为:(x-3)3.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
9.设x,y满足约束条件$\left\{\begin{array}{l}{x≤0}\\{2x+y≥1}\\{x+y≤2}\end{array}\right.$,则z=3x+y的最小值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.四条直线每两条都相交,且任三条都不交于一点,它们可确定的平面个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.若函数f(x)是一次函数,且函数图象经过点(0,1),(-1,3),则f(x)的解析式为( )
| A. | f(x)=2x-1 | B. | f(x)=2x+1 | C. | f(x)=-2x-1 | D. | f(x)=-2x+1 |
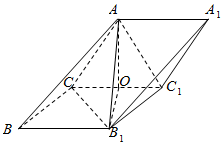 如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.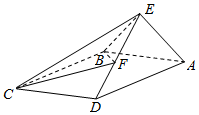 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.