题目内容
16.在△ABC中,A=120°,AB=4,若点D在边BC上,且BD=2DC,AD=$\frac{{2\sqrt{7}}}{3}$,则AC的长为3.分析 画出图形,结合图形,利用BD=2DC,得出$\overrightarrow{AD}$-$\overrightarrow{AB}$=2($\overrightarrow{AC}$-$\overrightarrow{AD}$),再利用平面向量的数量积求出|$\overrightarrow{AC}$|即可.
解答  解:如图所示:
解:如图所示:
△ABC中,∠BAC=120°,AB=4,点D在边BC上,BD=2DC,
∴$\overrightarrow{AD}$-$\overrightarrow{AB}$=2($\overrightarrow{AC}$-$\overrightarrow{AD}$),
∴3$\overrightarrow{AD}$=2$\overrightarrow{AC}$+$\overrightarrow{AB}$,
两边平方得9$\overrightarrow{AD}$2=4$\overrightarrow{AC}$2+4$\overrightarrow{AC}$•$\overrightarrow{AB}$+$\overrightarrow{AB}$2,
又AD=$\frac{{2\sqrt{7}}}{3}$,
∴9×($\frac{{2\sqrt{7}}}{3}$)2=4$\overrightarrow{AC}$2+4×|$\overrightarrow{AC}$|×4×cos120°+42,
化简得|$\overrightarrow{AC}$|2-2|$\overrightarrow{AC}$|-3=0,
解得|$\overrightarrow{AC}$|=3或|$\overrightarrow{AC}$|=-1(不合题意舍去),
故答案为:3.
点评 本题考查了利用平面向量的线性运算与数量积运算求三角形边长的应用问题.

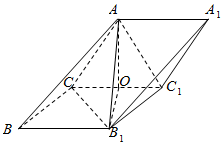 如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AC=AC1=B1C=B1C1=2,AC⊥AC1,B1C⊥B1C1,O为CC1的中点.