题目内容
如图，在半径为2| 3 |
（Ⅰ）按下列要求求出函数关系式并写出定义域：
①设PN=x，将y表示成x的函数关系式；
②设∠POB=θ，将y表示成θ的函数关系式．
（Ⅱ）请你选用（Ⅰ）中的一个函数关系式，求y的最大值．
考点：弧度制的应用
专题：计算题,三角函数的求值
分析：（Ⅰ）①求出MN，PN可将y表示成x的函数关系式；②在Rt△PON中，利用直角三角形中的边角关系求得 PN=Rsinθ，ON=Rcosθ，以及MQ和OM，可得关于矩形的面积S的解析式，化简可得结果；
（2）由②得y=6sin2θ-2
(1-cos2θ)=4
sin(2θ+
)-2
，故当θ=
时，y取得最大值．
（2）由②得y=6sin2θ-2
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
解答：
解：（1）①因为QM=PN=x，所以OM=
=
，又ON=
，
所以MN=ON-OM=
-
，
故y=MN•PN=x•
-
（0＜x＜3），
②当∠POB=θ时，QM=PN=2
sinθ，则OM=
=2sinθ，又ON=2
cosθ，
所以MN=ON-OM=2
cosθ-2sinθ，
故y=MN•PN=12sinθcosθ-4
sin2θ（0＜θ＜
）；
（2）由②得y=6sin2θ-2
(1-cos2θ)=4
sin(2θ+
)-2
，
故当θ=
时，y取得最大值为2
．
| QM |
| tan600 |
| x | ||
|
| 12-x2 |
所以MN=ON-OM=
| 12-x2 |
| x | ||
|
故y=MN•PN=x•
| 12-x2 |
| ||
| 3 |
②当∠POB=θ时，QM=PN=2
| 3 |
| QM |
| tan600 |
| 3 |
所以MN=ON-OM=2
| 3 |
故y=MN•PN=12sinθcosθ-4
| 3 |
| π |
| 3 |
（2）由②得y=6sin2θ-2
| 3 |
| 3 |
| π |
| 6 |
| 3 |
故当θ=
| π |
| 6 |
| 3 |
点评：本题主要考查直角三角形中的边角关系，三角函数的恒等变换，正弦函数的定义域和值域，属于中档题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
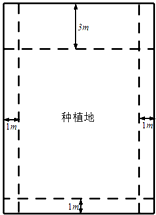某部队驻扎在青藏高原上，那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜，生活条件极为艰苦．但战士们不计个人得失，扎根风雪高原，以钢铁般的意志，自力更生，克服恶劣的自然环境．该部队现计划建造一个室内面积为800m2的矩形蔬菜温室，在温室内，与左、右两侧及后侧的内墙各保留1m宽的通道，与前侧内墙保留3m宽的空地．当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？
如图，四棱锥S-ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC⊥平面SBC．