题目内容
20．若一个圆台的轴截面如图所示，则其侧面积等于（ ）
| A． | 6 | B． | 6π | C． | $3\sqrt{5}π$ | D． | $6\sqrt{5}π$ |
分析 由圆台的轴截面可以看出圆台是一个下底面直径是4，上底面直径是2，圆台的高是2，根据这三个数据可以在轴截面上过上底的顶点向下底做垂线，根据勾股定理写出圆台的母线长，利用侧面积公式得到结果．
解答 解：由圆台的轴截面可以看出圆台是一个下底面直径是4，
上底面直径是2，圆台的高是2，
∴根据这三个数据可以写出圆台的母线长是$\sqrt{4+1}$=$\sqrt{5}$，
∴圆台的侧面积是S=$π×1×\sqrt{5}+π×2×\sqrt{5}$=3$\sqrt{5}$π，
故选C．
点评 本题考查空间图形的轴截面，考查圆台的侧面积公式，考查圆台的轴截面的用法，本题是一个基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
10．若实数a，b，c满足loga3＜logb3＜logc3，则下列关系中不可能成立的（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜b＜a | D． | a＜c＜b |
11．若集合A={x|mx2-2x+1=0}中只有一个元素，则实数m的值为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 0或1 |
15．已知三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且PA=2，PB=$\sqrt{3}$，PC=3，则这个三棱锥的外接球的表面积为（ ）
| A． | 16π | B． | 32π | C． | 36π | D． | 64π |
5．
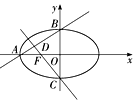如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）
如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）| A． | 3$\sqrt{3}$ | B． | -3$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{5}$ | D． | -$\frac{\sqrt{3}}{5}$ |
12．复数$z=\frac{4}{1+i}$（i是虚数单位）的共轭复数在复平面内对应的点是（ ）
| A． | （2，-2） | B． | （2，2） | C． | （-2，-2） | D． | （-2，2） |