题目内容
15.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,<$\overrightarrow{a}$,$\overrightarrow{b}$>=60°,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )| A. | 6 | B. | 3 | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 直接利用向量的数量积的运算法则求解即可.
解答 解:|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,<$\overrightarrow{a}$,$\overrightarrow{b}$>=60°,则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=2×$3×\frac{1}{2}$=3.
故选:B.
点评 本题考查向量的数量积的运算,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在下列直线中,与直线x+3y一4=0相交的直线为( )
| A. | x+3y=0 | B. | y=-$\frac{1}{3}x$-12 | C. | $\frac{x}{2}+\frac{y}{3}$=1 | D. | y=-$\frac{1}{3}$x+4 |
4.过点M(-2,a),N(a,4)的直线的斜率为-$\frac{1}{2}$,则|MN|=( )
| A. | 10 | B. | 180 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{5}$ |
5.定义在R上的函数f(x)满足f(-x)+f(x)=0,f(x)=-f(x+2),且x∈(-1,0)时,f(x)=2x-$\frac{1}{5}$,则f(log220)=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
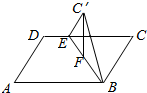 已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.