题目内容
6.证明:π为函数f(x)=sin(2x+$\frac{π}{6}$)的一个周期.分析 直接利用周期函数的定义证明.
解答 证明:∵f(π+x)=sin[2(π+x)+$\frac{π}{6}$]
=sin(2π+2x+$\frac{π}{6}$)=sin(2x+$\frac{π}{6}$)=f(x).
∴π为函数f(x)=sin(2x+$\frac{π}{6}$)的一个周期.
点评 本题考查三角函数的周期性,考查了周期函数的定义,是基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.已知数列{an}满足an=$\left\{\begin{array}{l}{(1-2a)n+1,n>3}\\{{a}^{n-2},1≤n≤3}\end{array}\right.$(n∈N*),若对于任意的n∈N*都有an>an+1,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{5}{9}$) | C. | ($\frac{1}{2}$,$\frac{5}{9}$) | D. | ($\frac{5}{9}$,1) |
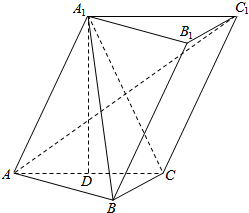 已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1