题目内容
已知函数f(x)=x3+x,对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,则x的取值范围为________.
 .
.
【解析】∵f′(x)=3x2+1>0恒成立,
∴f(x)在R上是增函数.
又f(-x)=-f(x),∴y=f(x)为奇函数.
由f(mx-2)+f(x)<0得f(mx-2)<-f(x)=f(-x),
∴mx-2<-x,即mx-2+x<0在m∈[-2,2]上恒成立.
记g(m)=xm-2+x,


练习册系列答案
相关题目
某学校为响应省政府号召,每学期派老师到各个民工子弟学校支教,以下是该学校50名老师上学期在某一个民工子弟学校支教的次数统计结果:
| 支教次数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
根据上表信息解答以下问题:
(1)从该学校任选两名老师,用η表示这两人支教次数之和,记“函数f(x)=x2-ηx-1在区间(4,5)上有且只有一个零点”为事件A,求事件A发生的概率P1;
(2)从该学校任选两名老师,用ξ表示这两人支教次数之差的绝对值,求随机变量ξ的分布列及数学期望E(ξ).
已知函数 ,则
,则 的值是( )
的值是( )
|
| A. | 9 | B. | ﹣9 | C. |
| D. |
|
设x,y满足约束条件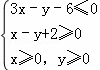 ,若目标函数z=ax+by(a>0,b>0)的最大值为12,则
,若目标函数z=ax+by(a>0,b>0)的最大值为12,则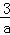 +
+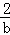 的最小值为( )
的最小值为( )
|
| A. | 4 | B. |
| C. | 1 | D. | 2 |
函数f(x)=log2(1+x),g(x)=log2(1﹣x),则f(x)﹣g(x)是( )
|
| A. | 奇函数 | B. | 偶函数 |
|
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
 的焦点到准线的距离是( )
的焦点到准线的距离是( ) D.
D.



 ,函数
,函数 .
. 时,写出
时,写出 的增区间;
的增区间; ,求
,求 ,使函数
,使函数 在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求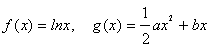
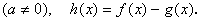
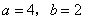 时,求
时,求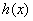 的极大值点;
的极大值点;  的图象
的图象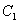 与函数
与函数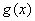 的图象
的图象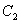 交于
交于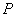 、
、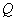 两点,过线段
两点,过线段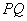 的中点做
的中点做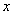 轴的垂线分别交
轴的垂线分别交 、
、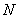 ,证明:
,证明: , 则
, 则 的值是
的值是