题目内容
设等比数列{an}的前n项和为Sn，且S2=1，S4=3，则S6=（ ）
| A、5 | B、7 | C、9 | D、11 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，代入数据计算可得．
解答：
解：由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，
即1，3-1，S6-3成等比数列，
∴22=1×（S6-3），解得S6=7．
故选：B．
即1，3-1，S6-3成等比数列，
∴22=1×（S6-3），解得S6=7．
故选：B．
点评：本题考查等比数列的性质，得出S2，S4-S2，S6-S4成等比数列是解决问题的关键，属中档题．
练习册系列答案
发散思维新课堂系列答案
相关题目
已知α为锐角，cos（α+
）=
，则sinα=（ ）
| π |
| 6 |
| 2 |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图是一个算法的流程图．若输入x的值为2，则输出y的值是（ ）
| A、0 | ||
B、-
| ||
| C、-1 | ||
D、-
|
过曲线y=
x3上的点P的切线l的方程为12x-3y=16，那么P点坐标可能为（ ）
| 1 |
| 3 |
A、（1，-
| ||
B、（2，
| ||
C、（-1，-
| ||
D、（3，
|
已知点A（a，b），B（x，y）为抛物线y=x2上两点，且x＞a，记|AB|=g（x）．若函数g（x）在定义域（a，+∞）上单调递增，则点A的坐标不可能是（ ）
| A、（1，1） |
| B、（0，0） |
| C、（-1，1） |
| D、（-2，4） |
已知角α终边上异于原点一点P且|PO|=r，则P点坐标为（ ）
| A、P（sinα，cosα） |
| B、P（cosα，sinα） |
| C、P（rsinα，rcosα） |
| D、P（rcosα，rsinα） |
某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．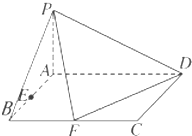
已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是线段AB，BC的中点，