题目内容
14.对某种电子元件进行寿命追踪调查,情况如下:| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
(2)估计该电子元件寿命的平均值.
分析 (1)根据表中数据,列出频率分布表,根据频率分布表,画出频率分布直方图;
(2)由频率分布表,计算该电子元件寿命的平均值即可.
解答 解:(1)根据表中数据,列出频率分布表如下;
| 分组(h) | 频数 | 频率 |
| 100~200 | 20 | 0.10 |
| 200~300 | 30 | 0.15 |
| 300~400 | 80 | 0.40 |
| 400~500 | 40 | 0.20 |
| 500~600 | 30 | 0.15 |
| 合计 | 200 | 1.00 |
(2)由频率分布表可知:

估计该电子元件寿命的平均值为
$\overline{x}$=$\frac{1}{200}$×(20×150+30×250+80×350+40×450+30×550)=365…(12分)
点评 本题考查了频率分布直方图与求平均数的应用问题,是基础题.

练习册系列答案
相关题目
4.若sin($\frac{π}{4}$-α)=$\frac{3}{5}$,-$\frac{π}{4}$<α<0,则cos2α=( )
| A. | -$\frac{24}{25}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{24}{25}$ |
5.函数f(x)=x3-3ax2+(2a+1)x既有极小值又有极大值,则a的取值范围为( )
| A. | -$\frac{1}{3}$<a<1 | B. | a>1或a$<-\frac{1}{3}$ | C. | -1$<a<\frac{1}{3}$ | D. | a$>\frac{1}{3}$或a<-1 |
6.如图,小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )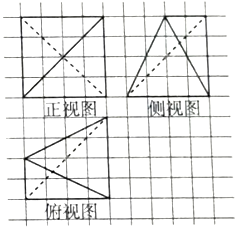

| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
4.如图为体积是3的几何体的三视图,则正视图的x值是( )
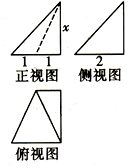

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |