题目内容
19.已知(x3+$\frac{1}{x^2}$)n的展开式中,只有第六项的二项式系数最大,求展开式中不含x的项.分析 由(x3+$\frac{1}{x^2}$)n展开式中只有第六项的二项式系数最大,可得n=10.再利用通项公式即可得出展开式中不含x的项.
解答 解:∵(x3+$\frac{1}{x^2}$)n的展开式中,只有第六项的二项式系数最大,∴n=10.
∴(x3+$\frac{1}{x^2}$)10的通项公式为:Tr+1═${C}_{10}^{r}{x}^{30-5r}$,
令30-5r=0,解得r=6.
∴展开式的不含x的项=${C}_{10}^{6}$=210.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知α是△ABC的一个内角,且$sinα+cosα=\frac{1}{5}$,
(Ⅰ)判断△ABC的形状;
(Ⅱ)求$\frac{{sinxcosx+{{sin}^2}x}}{1-tanx}$的值.
(Ⅰ)判断△ABC的形状;
(Ⅱ)求$\frac{{sinxcosx+{{sin}^2}x}}{1-tanx}$的值.
7.如图所示,两个阴影部分的面积之和可表示为( )
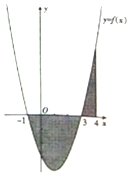

| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
14.对某种电子元件进行寿命追踪调查,情况如下:
(1)画出频率分布直方图;
(2)估计该电子元件寿命的平均值.
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
(2)估计该电子元件寿命的平均值.