题目内容
13.设函数f(x)=2x3+3ax2+3bx+c在x=1及x=2时取得极值.(1)求a,b的值;
(2)若f(x)在[-1,2]上的最大值是9,求f(x)在[-1,2]上的最小值.
分析 (1)求出函数的导数,利用函数的极值,列出方程组求解a,b即可.
(2)利用函数的导数,判断函数的单调性求出函数的最大值,推出c,然后求解函数的最小值即可.
解答 解:(1)函数f(x)=2x3+3ax2+3bx+c,可得f′(x)=6x2+6ax+3b
因为函数f(x)在x=1及x=2时取得极值,则有f′(1)=0,f′(2)=0.
即$\left\{\begin{array}{l}{6+6a+3b=0}\\{24+12a+3b=0}\end{array}\right.$解得a=-3,b=4.
(2)由(1)可知,f(x)=2x3-9x2+12x+c,f′(x)=6x2-18x+12=6(x-1)(x-2).
当x∈[-1,1]时,f′(x)>0;当x∈(1,2]时,f′(x)<0.
f(x)在[-1,2]上的最大值是f(1)=5+c=9,c=4.
此时f(-1)=-19,f(2)=8,所以最小值在x=-1时取得,为-19.
点评 本题考查函数的极值的求法函数的单调性以及函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
3.若△ABC的内角A,B,C的对边分别为a,b,c,已知2bsin2A=asinB,且c=2b,则$\frac{a}{b}$=( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
1.已知$\overrightarrow a$•$\overrightarrow b$=-6,$|{\overrightarrow a}|=4$,$|{\overrightarrow b}|=3$,则$\overrightarrow a$在$\overrightarrow b$方向上的投影是( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | -2 | D. | -6 |
8.若f(x)在R上可导,$f(x)={x^2}+2f'(\frac{π}{2})x+sin2x$,则$\int_0^1{f(x)dx}$=( )
| A. | $\frac{7}{3}-π-cos2$ | B. | $\frac{11}{6}-π+\frac{1}{2}cos2$ | C. | $\frac{17}{6}-π-\frac{1}{2}cos2$ | D. | $\frac{11}{6}-π-\frac{1}{2}cos2$ |
18.某程序框图如图所示,若t=7,则输出的值为( )
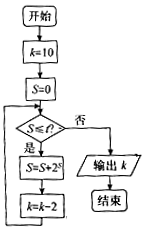

| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
3.将函数$f(x)=2cos(\frac{x}{2}-\frac{π}{6})$的图象向左平移$\frac{π}{3}$单位后得到函数g(x)的图象,则函数g(x)在[-π,4π]上的图象与直线y=1的交点的横坐标之和为( )
| A. | 2π | B. | 3π | C. | $\frac{10π}{3}$ | D. | $\frac{11π}{3}$ |