题目内容
5.已知函数f(x)=$\frac{1}{2}$x2-ax+(3-a)lnx,a∈R.(1)若曲线y=f(x)在点(1,f(1))处的切线与直线2x-y+1=0垂直,求a的值;
(2)设f(x)有两个极值点x1,x2,且x1<x2,求证:f(x1)+f(x2)>-5.
分析 (1)根据导数的几何意义即可求出a的值,
(2)根据x1,x2为f′(x)=0的两根,求出a的范围,再根据韦达定理得到f(x1)+f(x2)=-$\frac{1}{2}$a2+a-3+(3-a)ln(3-a),构造函数h(a)=-$\frac{1}{2}$a2+a-3+(3-a)ln(3-a),a∈(2,3),求出函数的最小值大于5即可.
解答 解:(1)∵f′(x)=x-a+$\frac{3-a}{x}$=$\frac{{x}^{2}-ax+3-a}{x}$,
∴k=f′(1)=4-2a,
∵曲线y=f(x)在点(1,f(1))处的切线与直线2x-y+1=0垂直,
∴k=-$\frac{1}{2}$,
∴4-2a=-$\frac{1}{2}$,
解得a=$\frac{9}{4}$
(2)由题意,x1,x2为f′(x)=0的两根,
∴$\left\{\begin{array}{l}{{a}^{2}-4(3-a)>0}\\{a>0}\\{3-a>0}\end{array}\right.$,
∴2<a<3,
又∵x1+x2=a,x1x2=3-a,
∴f(x1)+f(x2)=$\frac{1}{2}$(x12+x22)-a(x1+x2)+(3-a)lnx1x2,
=f(x)=-$\frac{1}{2}$a2+a-3+(3-a)ln(3-a),
设h(a)=-$\frac{1}{2}$a2+a-3+(3-a)ln(3-a),a∈(2,3),
则h′(a)=-a-ln(3-a),
∴h″(a)=-1+$\frac{1}{3-a}$=$\frac{a-2}{3-a}$>0,
故h′(a)在(2,3)递增,又h′(2)=-2<0,
当a→3时,h′(a)→+∞,
∴?a0∈(2,3),
当a∈(2,a0)时,h(a)递减,当a∈(a0,3)时,h(a)递增,
∴h(a)min=h(a0)=-$\frac{1}{2}$a02+a0-3+(3-a0)ln(3-a0)>-$\frac{1}{2}$a02+a0-3+(3-a0)(-a0)=$\frac{1}{2}$a02-2a0-3=$\frac{1}{2}$(a0-2)2-5>-5.
∴?a∈(2,3),h(a)>-5,
综上,f(x1)+f(x2)>-5.
点评 本题考查利用导数研究函数的极值,考查不等式的证明,考查学生分析解决问题的能力,属于难题.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案| A. | $({\frac{1}{27},+∞})$ | B. | $({\frac{4}{27},+∞})$ | C. | $[{\frac{1}{27},+∞})$ | D. | $[{\frac{4}{27},+∞})$ |
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
| A. | 类比推理是由特殊到特殊的推理 | |
| B. | 归纳推理是由特殊到一般的推理 | |
| C. | 演绎推理是由一般到特殊的推理 | |
| D. | 合情推理和演绎推理所得的结论都是正确的 |
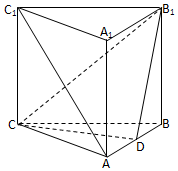 如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点
如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点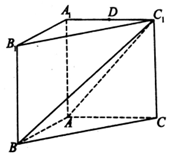 如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C
如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C