题目内容
1.已知$\overrightarrow a$•$\overrightarrow b$=-6,$|{\overrightarrow a}|=4$,$|{\overrightarrow b}|=3$,则$\overrightarrow a$在$\overrightarrow b$方向上的投影是( )| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | -2 | D. | -6 |
分析 可以得出$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$,而条件中已知$\overrightarrow{a}•\overrightarrow{b}=-6,|\overrightarrow{b}|=3$,从而可得出该投影的值.
解答 解:$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为:
$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=|\overrightarrow{a}|•\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$
=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$
=$\frac{-6}{3}$
=-2.
故选C.
点评 考查向量夹角的余弦公式,投影的定义及计算公式.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
12.2016年春运期间为查醉酒驾驶,将甲、乙、丙三名交警安排到某商业中心附近的两个不同路口突击检查,每个路口至少一人,则甲、乙两名交警不在同一路口的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
10.已知A(1,0),B(2,4),则$\overrightarrow{AB}$=( )
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
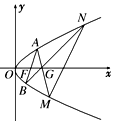 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).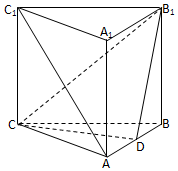 如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点
如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点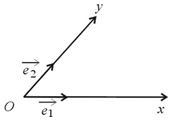 如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.
如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.