Question

对下面四个命题：
①若A、B、U为集合，A⊆U，B⊆U，A∩B=A，则∁_UA⊆∁_UB；
②二项式（2x-

1

x2

）⁶的展开式中，其常数项是240；
③对直线l、m，平面α、β，若l∥α，l∥β，α∩β=m，则l∥m；
④函数y=（x+1）²+1，（x≥0）与函数y=-1+

x-1

，（x≥1）互为反函数．
其中正确命题的序号是

 

．

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：画图判断①错误；由二项式的通项求出常数项说明②正确；直接证明③正确；求出函数的反函数说明④错误．

解答： 解：对于①，如图，

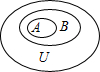
若A、B、U为集合，A⊆U，B⊆U，A∩B=A，则∁_UB⊆∁_UA，①错误；
②二项式（2x-

1

x2

）⁶的展开式中，由Tr+1=

C

r 6

(2x)6-r•(-

1

x2

)r=(-1)r26-r

C

r 6

x6-3r，
由6-3r=0，得r=2．
∴其常数项是(-1)224

C

2 6

=240，②正确；
③对直线l、m，平面α、β，若l∥α，l∥β，α∩β=m，
如图，

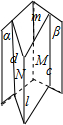
过l分别作平面M，N交β，α于c，d，由线面平行的性质得c∥d，则c∥α，再由线面平行的性质得c∥m，
由平行公理可得l∥m，③正确；
对于④，由y=（x+1）²+1，（x≥0），得x=-1+

y-1

，（y≥2），
x与y互换得：y=-1+

x-1

，（x≥2）．
∴函数y=（x+1）²+1，（x≥0）的反函数为y=-1+

x-1

，（x≥2），④错误．
∴正确的命题是②③．
故答案为：②③．

点评：本题考查了命题的真假判断与应用，考查了集合间的关系的判断，考查了二项式定理的应用及函数反函数的求法，训练了线面平行与性质的应用，是中档题．