题目内容
设双曲线
+
=1的离心率为2,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程为( )
| x2 |
| m |
| y2 |
| n |
A、
| ||||
B、
| ||||
C、y2-
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点,可得双曲线的c=2,且焦点在y轴上,由双曲线的离心率公式和a,b,c的关系,解方程可得m,n,进而得到双曲线方程.
解答:
解:抛物线x2=8y的焦点为(0,2),
则双曲线的焦点在y轴上,方程为
-
=1,
则c=2=
,
双曲线
+
=1的离心率为2,
则
=2,
解得m=-3,n=1.
即有双曲线的方程为y2-
=1.
故选C.
则双曲线的焦点在y轴上,方程为
| y2 |
| n |
| x2 |
| -m |
则c=2=
| n-m |
双曲线
| x2 |
| m |
| y2 |
| n |
则
| ||
|
解得m=-3,n=1.
即有双曲线的方程为y2-
| x2 |
| 3 |
故选C.
点评:本题考查抛物线和双曲线的方程和性质,主要考查双曲线的离心率和a,b,c的关系,属于基础题.

练习册系列答案
相关题目
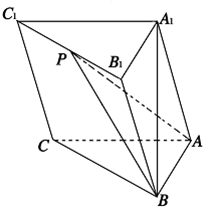 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=