题目内容
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2006,则i、j的值分别为( )
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2006,则i、j的值分别为( )| A、64,53 |
| B、63,53 |
| C、63,54 |
| D、64,54 |
考点:归纳推理
专题:规律型,等差数列与等比数列
分析:第一行有一个数,第二行有两个数…,第n行有n个数字,这样每一行的数字个数组成一个等差数列,表示出等差数列的前项和,使得和大于或等于2006,解出不等式,做出n的值,在满足条件的数字附近检验,得到结果.
解答:
解:由题意可知,第一行有一个数,第二行有两个数,第三行有三个数,…,
第62行有62个数,第63行有63个数,第n行有n个数字,
这样每一行的数字个数组成一个等差数列,
∴前n项的和是
,
∴
≥2006,
∴(n+64)(n-63)≥0
∴n≥63或n≤-64(舍去)
当n=63时,
=2016
∴a63,53=(1+2+3+…+62)+53=
(1+62)+53=2006.
故i、j的值分别为:63;53,
故选:B
第62行有62个数,第63行有63个数,第n行有n个数字,
这样每一行的数字个数组成一个等差数列,
∴前n项的和是
| n(n+1) |
| 2 |
∴
| n(n+1) |
| 2 |
∴(n+64)(n-63)≥0
∴n≥63或n≤-64(舍去)
当n=63时,
| 63(63+1) |
| 2 |
∴a63,53=(1+2+3+…+62)+53=
| 62 |
| 2 |
故i、j的值分别为:63;53,
故选:B
点评:本题考查数列的性质和应用,本题解题的关键是看出所形成的数列是一个等差数列,后面的问题按照等差数列来解题.

练习册系列答案
相关题目
过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆方程为( )
A、(x+
| ||||||
B、(x-
| ||||||
C、(x-
| ||||||
D、(x+
|
工人师傅想对如图1的直角铁皮,用一条直线m将其分成面积相等的两部分.图2是甲、乙、丙、丁四位同学给出的做法,其中做法正确的学生数是( )
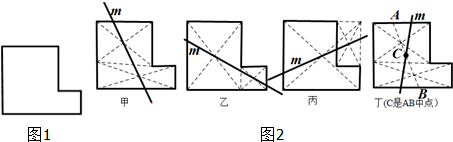

| A、4个 | B、3个 | C、2个 | D、1个 |
如图是某条公共汽车线路收支差额y与乘客量x的图象(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格.下面给出四个图象:在这些图象中( )


| A、①反映了建议(Ⅱ),③反映了建议(Ⅰ) |
| B、①反映了建议(Ⅰ),③反映了建议(Ⅱ) |
| C、②反映了建议(Ⅰ),④反映了建议(Ⅱ) |
| D、④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
抛物线y2=8x与双曲线
-
=1的一个焦点重合,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
已知复数z满足(2-i)z=4+3i(i为虚数单位),则|z-i|=( )
A、
| ||
B、
| ||
C、2
| ||
D、2
|
下面几种推理过程是演绎推理的是( )
| A、由6=3+3,8=3+5,10=3+7,12=5+7,14=7+7,…,得出结论:一个偶数(大于4)可以写成两个素数的和. | ||||
| B、两条直线平行,两同旁内角互补,因为∠A和∠B是两条平行直线的同旁内角,所以∠A+∠B=180° | ||||
| C、我国地质学家李四光发现中国松辽地区和中亚细亚的地质结构类似,而中亚细亚有丰富的石油,由此,他推断松辽平原也蕴藏着丰富的石油 | ||||
D、在数列{an}中,a1=1,an=
|
复数z满足|z|=2,则|z-3-4i|的取值范围是( )(i为虚数单位)
| A、(1,3) |
| B、[1,3] |
| C、(3,7) |
| D、[3,7] |