题目内容
工人师傅想对如图1的直角铁皮，用一条直线m将其分成面积相等的两部分．图2是甲、乙、丙、丁四位同学给出的做法，其中做法正确的学生数是（ ）
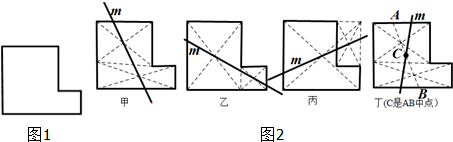
| A、4个 | B、3个 | C、2个 | D、1个 |
考点：进行简单的合情推理
专题：规律型
分析：根据图形中所画出的虚线，可以利用图形中的长方形、梯形的面积比较得出直线两旁的面积的大小关系．
解答：
解：如图：图形（1）中，直线m经过了大长方形和小长方形的对角线的交点，所以两旁的图形的面积都是大长方形和小长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即甲做法正确；
图形（2）中，直线m经过大正方形和小长方形的对角线的交点，所以两旁的图形的面积都是大长方形和小长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即乙做法正确；
图形（3）中，经过大正方形和图形外不添补的长方形的对角线的交点，直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即丙做法正确；
图形（4）中，直线m经过AB的中点，由（1）知，AB平分图形面积，而直线m与AB相交所截得的两个三角形全等，故割补后，这条直线把这个图形分成了面积相等的两部分，即丁做法正确；
故其中分法正确的学生有4个，
故选：A
图形（2）中，直线m经过大正方形和小长方形的对角线的交点，所以两旁的图形的面积都是大长方形和小长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即乙做法正确；
图形（3）中，经过大正方形和图形外不添补的长方形的对角线的交点，直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半，所以这条直线把这个图形分成了面积相等的两部分，即丙做法正确；
图形（4）中，直线m经过AB的中点，由（1）知，AB平分图形面积，而直线m与AB相交所截得的两个三角形全等，故割补后，这条直线把这个图形分成了面积相等的两部分，即丁做法正确；
故其中分法正确的学生有4个，
故选：A
点评：根据图形中的割补情况，抓住经过对角线的交点的直线都能把长方形分成面积相等的两部分这一特点，即可解决问题．
练习册系列答案
全优点练单元计划系列答案
相关题目
f（x）=2sinπx-x+1的零点个数为（ ）
| A、4 | B、5 | C、6 | D、7 |
λ，μ∈R，下面式子正确的是（ ）
A、λ
| ||||||||
B、（λ+μ）
| ||||||||
C、0•
| ||||||||
D、若
|
若f（x）在[a，b]上连续，在（a，b）内可导，且x∈（a，b）时，f′（x）＞0，又f（a）＜0，则（ ）
| A、f（x）在[a，b]上单调递增，且f（b）＞0 |
| B、f（x）在[a，b]上单调递增，且f（b）＜0 |
| C、f（x）在[a，b]上单调递减，且f（b）＜0 |
| D、f（x）在[a，b]上单调递增，但f（b）的符号无法判断 |
设x，y满足约束条件
，则z=（x+1）2+（y-1）2的最小值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
在正项等比数列{an}中，已知a3•a5=12，则a1+a7的最小值为（ ）
A、4
| ||
B、2
| ||
C、2
| ||
D、4
|
把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8．若ai，j=2006，则i、j的值分别为（ ）| A、64，53 |
| B、63，53 |
| C、63，54 |
| D、64，54 |
长方体的一个顶点上三条棱长分别是2，4，
，且它的8个顶点都在同一球面上，则这个球的表面积是（ ）
| 5 |
| A、25π | B、50π |
| C、125π | D、都不对 |