题目内容
已知a，b，c均为正实数，且a+b+c=1．求
+
+
的最大值．
| 4a+1 |
| 4b+1 |
| 4c+1 |
考点：二维形式的柯西不等式
专题：计算题,不等式
分析：利用柯西不等式得（a2+b2+c2）（m2+n2+p2）≥（am+bn+cp）2进行求解即可．
解答：
解：由柯西不等式得（
+
+
）2≤（12+12+12）（4a+1+4b+1+4c+1）
=3[4（a+b+c）+3]=21…（5分）
当且仅当a=b=c=
时等号成立
故
+
+
的最大值为
．
| 4a+1 |
| 4b+1 |
| 4c+1 |
=3[4（a+b+c）+3]=21…（5分）
当且仅当a=b=c=
| 1 |
| 3 |
故
| 4a+1 |
| 4b+1 |
| 4c+1 |
| 21 |
点评：利用柯西不等式时，关键是如何凑成能利用一般形式的柯西不等式的形式，属于中档题．
练习册系列答案
相关题目
已知实数x，y满足条件
，则y-（
）x的最大值为（ ）
|
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
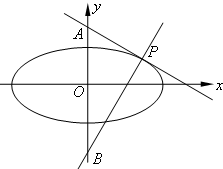椭圆C：