题目内容
函数y=3-2sin22x的最小正周期为（ ）
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
考点：二倍角的余弦,三角函数的周期性及其求法
专题：计算题,三角函数的图像与性质
分析：先将函数运用二倍角公式化简为y=Asin（wx+φ）的形式，再利用正弦函数的性质可得答案．
解答：
解：由题意可得：f（x）=2+cos4x，
所以周期为T=
=
．
故选：A．
所以周期为T=
| 2π |
| 4 |
| π |
| 2 |
故选：A．
点评：本题主要考查三角函数的最小正周期的求法．一般都要把三角函数化简为y=Asin（wx+φ）的形式再解题．
练习册系列答案
名校课堂系列答案
相关题目
某校为了解网瘾学生上网情况，抽查了100名同学，统计他们暑假期间每天平均上网时间，绘成频率分布直方图（如图）．则这100名同学中每天平均上网时间在6～8小时内的同学人数为（ ）| A、30 | B、40 | C、50 | D、60 |
已知实数x，y满足条件
，则y-（
）x的最大值为（ ）
|
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
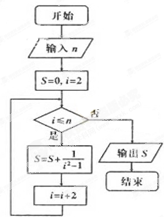
如图所示的程序框图，则输出的结果为（ ）
| A、189 | B、381 |
| C、93 | D、45 |
函数f（x）=sinx（x∈[0，π]），在区间[0，π]上任取一点x0，则f（x0）≥
的概率为（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x、y满足约束条件
，若向量
=（x，y），向量
=（3，-1）．设z表示向量
在向量
方向上的投影，则z的最大值是（ ）
|
| a |
| b |
| a |
| b |
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、6 |
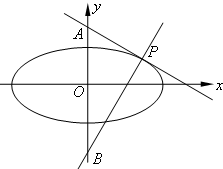椭圆C：