题目内容
已知矩阵M＝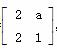
，其中a∈R，若点P(1，－2)在矩阵M的变换下得到点P′(－4，0)．
(1) 求实数a的值；
(2) 求矩阵M的特征值及其对应的特征向量．
解：(1) 由
得2－2a＝－4a＝3.
(2) 由(1)知M＝
，则矩阵M的特征多项式为f(λ)＝
＝(λ－2)(λ－1)－6＝λ2－3λ－4.令f(λ)＝0，得矩阵M的特征值为－1与4.
当λ＝－1时，
x＋y＝0，
∴ 矩阵M的属于特征值－1的一个特征向量为
；当λ＝4时，2x－3y＝0.∴ 矩阵M的属于特征值4的一个特征向量为
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的点的个数是________．
下，直线x＋y＝k(k为常数)上的所有点都变为一个点，求此点坐标．
的特征多项式．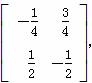
，求矩阵A的特征值．
(t为参数)，求直线的斜率．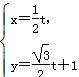
(t为参数)，求直线l被曲线C截得的线段的长度．