题目内容
7.已知数列{an}的前n项和为Sn,且${S_n}+\frac{1}{3}{a_n}=1$(n∈N+).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log4(1-Sn+1)(n∈N+),${T_n}=\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}$,求使${T_n}≥\frac{504}{1009}$成立的最小的正整数n的值.
分析 (Ⅰ)当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,结合等比数列的定义和通项公式计算即可得到所求;
(Ⅱ)运用等比数列的求和公式和对数的运算性质,可得bn,再由裂项相消求和方法,求得Tn,解不等式即可得到所求最小值.
解答 解:(Ⅰ)当n=1时,a1=S1,S1+$\frac{1}{3}$a1=1,解得a1=$\frac{3}{4}$,
当n≥2时,an=Sn-Sn-1=1-$\frac{1}{3}$an-(1-$\frac{1}{3}$an-1),
即为an=$\frac{1}{4}$an-1,
由a1+a2+$\frac{1}{3}$a2=1,
可得a2=$\frac{3}{16}$,
则an=a2•($\frac{1}{4}$)n-2=$\frac{3}{16}$•($\frac{1}{4}$)n-2=3•($\frac{1}{4}$)n,对n=1也成立,
可得数列{an}的通项公式为an=3•($\frac{1}{4}$)n;
(Ⅱ)bn=log4(1-Sn+1)=log4[1-$\frac{\frac{3}{4}(1-\frac{1}{{4}^{n+1}})}{1-\frac{1}{4}}$]
=log4$\frac{1}{{4}^{n+1}}$=-(n+1),
${T_n}=\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}$=$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{(n+1)(n+2)}$
=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$=$\frac{1}{2}$-$\frac{1}{n+2}$,
${T_n}≥\frac{504}{1009}$成立,即为$\frac{1}{2}$-$\frac{1}{n+2}$≥$\frac{504}{1009}$,
解得n≥2016,
则使${T_n}≥\frac{504}{1009}$成立的最小的正整数n的值为2016.
点评 本题考查数列的通项公式的求法,注意运用数列的递推式,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | [0,e3-4] | B. | [0,$\frac{1}{{e}^{3}}$+2] | C. | [$\frac{1}{{e}^{3}}$+2,e3-4] | D. | [e3-4,+∞) |
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
| A. | $\frac{{2\sqrt{6}}}{3}R$ | B. | $\frac{{\sqrt{6}}}{3}R$ | C. | R | D. | $\sqrt{6}R$ |
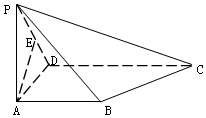 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.