题目内容
2．过点（0，4）且与抛物线y2=8x只有一个公共点的直线共有（ ）| A． | 0条 | B． | 1条 | C． | 2条 | D． | 3条 |
分析 直接分直线l的斜率存在和不存在，当斜率不存在和斜率存在等于0时记忆分析，当斜率存在不等于0时联立直线方程和抛物线方程后化为关于x的一元二次方程，由判别式等于0即可得到答案．
解答 解：若直线l的斜率不存在，则直线l的方程为x=0，满足条件；
当直线l的斜率存在时，不妨设l：y=kx+4，代入y2=8x，得：k2x2+（8k-8）x+16=0
由条件知，当k=0时，即：直线y=4与抛物线有一个交点；
当k≠0时，由△=（8k-8）2-4×16×k2=0，解得：k=$\frac{1}{2}$，则直线方程为y=$\frac{1}{2}$x+4
故满足条件的直线方程为：x=0或y=4或y=$\frac{1}{2}$x+4.3条．
故选：D．
点评 本题考查了直线和圆锥曲线的关系，考查了分类讨论的数学思想方法，训练了判别式法的方法，是中档题．
练习册系列答案
相关题目
6．已知向量$\overrightarrow{a}$=（m-1，2），$\overrightarrow{b}$=（m，-3），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数m等于（ ）
| A． | 2或-3 | B． | -2或3 | C． | $\frac{3}{5}$ | D． | 3 |
13．设点P为公共焦点F1（-2，0），F2（2，0）的椭圆和双曲线的一个交点，且cos∠F1PF2=$\frac{3}{5}$，已知椭圆的长轴长是双曲线实轴长的4倍，则双曲线的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\sqrt{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
10．把函数y=sin（2x+$\frac{π}{6}$）图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再将图象向右平移$\frac{π}{3}$个单位，得到函数y=g（x），那么g（$\frac{π}{3}$）的值为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
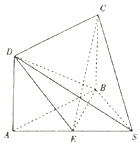如图，在四棱锥S-ABCD中，四边形为ABCD矩形，E为SA的中点，SA=SB，AB=2$\sqrt{3}$，BC=3．
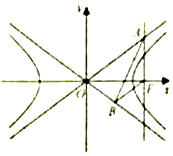如图，已知双曲线$C：\frac{x^2}{a^2}-{y^2}=1（a＞0）$的右焦点F，点A，B分别在C的两条渐近线上，AF⊥x轴，AB⊥OB，BF∥OA（O为坐标原点）．求双曲线C的方程．