题目内容
17.过M(-1,0)做抛物线C:y2=2px(p>0)的两条切线,切点分别为A,B.若$\overline{MA}•\overline{MB}=0$.(1)求抛物线C的方程;
(2)N(t,0),(t≥1),过N任做一直线交抛物线C于P,Q两点,当t也变化时,求|PQ|的最小值.
分析 (1)$\overline{MA}•\overline{MB}=0$⇒MA•MB=90°,由抛物线的对称性可得:KMA=1,直线l的方程与抛物线方程联立化为:y2-2px+2p=0.利用△=0,即可得出p.
(2)设PQ的方程为:x=my+t,代入抛物线方程可得y2-4my-4t=0,t≥1.△>0,设P(x1,y1),Q(x2,y2),y1+y2=4my,y1y2=-4t,$|{PQ}|=\sqrt{1+{m^2}}\sqrt{(1+m{)^2}+16t}$,即可得出.
解答 解:(1)$\overline{MA}•\overline{MB}=0$⇒MA•MB=90°,
由抛物线的对称性,∴KMA=1,
∴${l_{AM}}:\left\{{\begin{array}{l}{y=x+1}\\{{y^2}=2px}\end{array}}\right.$,
∴y2-2px+2p=0.
∴$\left.{\begin{array}{l}{△=4{p^2}-8p=0}\\{p>0}\end{array}}\right\}$,∴p=2.
∴y2=4x.
(2)设PQ的方程为:x=my+t,代入抛物线方程可得:y2-4my-4t=0,t≥1.△>0,
设P(x1,y1),Q(x2,y2),
∴y1+y2=4my,y1y2=-4t,
$|{PQ}|=\sqrt{1+{m^2}}\sqrt{(1+m{)^2}+16t}$=$4\sqrt{1+{m^2}}\sqrt{{m^2}+t}$,
∴m=0时,${|{PQ}|_{min}}=4\sqrt{t}$(t≥1).
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相切相交问题、一元二次方程的根与系数的关系、弦长公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
| A. | y3>y1>y2 | B. | y2>y1>y3 | C. | y1>y2>y3 | D. | y1>y3>y2 |
| A. | (-3,3) | B. | (-1,1) | C. | (-3,1) | D. | (-3,-1)∪(1,3) |
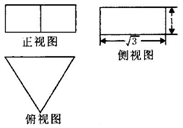
| A. | $6\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
| A. | 20 | B. | 24 | C. | 28 | D. | 34 |