题目内容
已知曲线x2+y+1=0与双曲线x2-
=1(b>0)的渐近线相切,则此双曲线的焦距等于( )
| y2 |
| b2 |
A、2
| ||
B、2
| ||
| C、4 | ||
D、2
|
考点:双曲线的简单性质
专题:计算题,导数的概念及应用,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,以及函数y=-x2-1的导数,设出切点,求出切线的斜率,得到方程,解方程即可得到切点和b的值,进而得到双曲线的c,即有焦距2c.
解答:
解:双曲线x2-
=1(b>0)的渐近线方程为y=±bx,
曲线x2+y+1=0,即为y=-x2-1,y′=-2x,
可设切点为(m,n),(m>0),
则-b=-2m,n=-m2-1,n=-bm,
解得,m=1,b=2,n=-2.
则双曲线的c=
=
,
则焦距为2
.
故选D.
| y2 |
| b2 |
曲线x2+y+1=0,即为y=-x2-1,y′=-2x,
可设切点为(m,n),(m>0),
则-b=-2m,n=-m2-1,n=-bm,
解得,m=1,b=2,n=-2.
则双曲线的c=
| 1+b2 |
| 5 |
则焦距为2
| 5 |
故选D.
点评:本题考查双曲线的方程和性质,考查导数的几何意义:曲线在该点处的切线的斜率,考查运算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知直线l1:2x-y+1=0,l2:x-3y-=0,则l1到l2的角是( )
| A、45° | B、60° |
| C、120° | D、135° |
湖面上飘着一个小球,湖水结冰后将球取出,冰面上留下一个半径为6cm,深2cm的空穴,则取出该球前,球面上的点到冰面的最大距离为( )
| A、20cm | B、18cm |
| C、10cm | D、8cm |
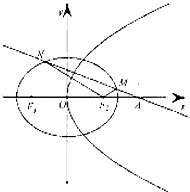 如图,己知椭圆C:
如图,己知椭圆C: