题目内容
已知关于x的不等式|x+1|+|x-2|≤(a+
)(
+b)对任意正实数a、b恒成立,求实数x的取值范围.
| 1 |
| b |
| 1 |
| a |
考点:绝对值不等式的解法
专题:不等式的解法及应用,不等式
分析:将不等式的右边化简,运用基本不等式可得最小值为4,则需解不等式|x+1|+|x-2|≤4,讨论当x≤-1时,当-1<x<2时,当x≥2时,去绝对值,解不等式,最后求并集即可.
解答:
解:由于a,b>0,(a+
)(
+b)=2+ab+
≥2+2
=4,当且仅当ab=1时取“=”号,
∴(a+
)(
+b)的最小值为4,
∴|x+1|+|x-2|≤4,
当x≤-1时,-x-1+2-x≤4,解得,x≥-
,则有-
≤x≤-1;
当-1<x<2时,x+1+2-x≤4,即3≤4成立,则有-1<x<2;
当x≥2时,x+1+x-2≤4,解得,x≤
,则有2≤x≤
.
综上x的取值范围是[-
,
].
| 1 |
| b |
| 1 |
| a |
| 1 |
| ab |
≥2+2
ab•
|
∴(a+
| 1 |
| b |
| 1 |
| a |
∴|x+1|+|x-2|≤4,
当x≤-1时,-x-1+2-x≤4,解得,x≥-
| 3 |
| 2 |
| 3 |
| 2 |
当-1<x<2时,x+1+2-x≤4,即3≤4成立,则有-1<x<2;
当x≥2时,x+1+x-2≤4,解得,x≤
| 5 |
| 2 |
| 5 |
| 2 |
综上x的取值范围是[-
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题考查绝对值不等式的解法,考查基本不等式的运用:求最值,考查不等式恒成立问题转化为求最值问题,考查运算能力,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
湖面上飘着一个小球,湖水结冰后将球取出,冰面上留下一个半径为6cm,深2cm的空穴,则取出该球前,球面上的点到冰面的最大距离为( )
| A、20cm | B、18cm |
| C、10cm | D、8cm |
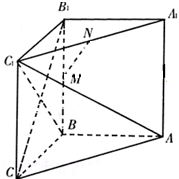 如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.
如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.