题目内容
19.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为$\frac{1}{2}$.分析 由已知式子平方可得cosθ的方程,解方程可得.
解答 解:设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,
∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
∴平方可得${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=|$\overrightarrow{a}$|2,
∴${\overrightarrow{b}}^{2}$=2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=2|$\overrightarrow{b}$|2cosθ
∴cosθ=$\frac{1}{2}$
故答案为:$\frac{1}{2}$
点评 本题考查数量积和向量的夹角,属基础题.

练习册系列答案
相关题目
9.函数f(x)=3x-2x-3的零点的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.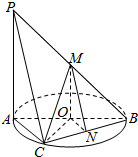 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
14.已知区间D⊆[0,2π],函数y=cosx在区间D上是增函数,函数y=sinx在区间D上是减函数,那么区间D可以是( )
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [π,$\frac{3π}{2}$] | D. | [$\frac{3π}{2}$,2π] |
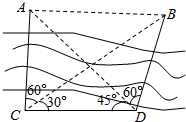 如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.
如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.