Question

8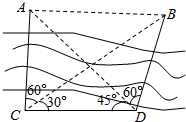．如图，A、B两点都在河的对岸（不可到达），测量者在河岸边选定两点C、D，测得CD=40m，并且在C、D两点分别测得∠ACB=60°，∠ADB=60°∠BCD=30°，∠ADC=45°，求河的对岸的两点A、B间的距离．

Answer 1

分析 分别在三角形ABC和三角形BCD中求出AD，BD，再在三角形ABD中使用余弦定理求出AB．

解答 解：∵∠CAB=180°-∠ADC-∠ACB=45°，∴△ABC是等腰直角三角形，∴AC=CD=40，AD=40$\sqrt{2}$．
在△BCD中，∠CBD=180°-∠BCD-∠BDC=45°，∵$\frac{BD}{sin30°}=\frac{CD}{sin45°}$，∴BD=20$\sqrt{2}$．
在△ABD中，由余弦定理得AB²=AD²+BD²-2AD•BD•cos60°=2400，
∴AB=20$\sqrt{6}$．

点评 本题考查了正余弦定理在解三角形中的应用，属于中档题．