题目内容
如图，正三棱锥A-BCD的底面边长为2，侧棱长为3，E为棱BC的中点．（1）求异面直线AE与CD所成角的大小（结果用反三角函数值表示）；
（2）求该三棱锥的体积V．
考点：异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题：空间角
分析：（1）根据异面直线所成角的定义即可求异面直线AE与CD所成角的大小；
（2）根据锥体的体积公式即可求该三棱锥的体积V．
（2）根据锥体的体积公式即可求该三棱锥的体积V．
解答：
解：（1）取BD中点F，连结AF、EF，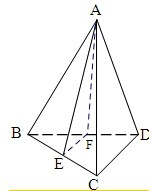
因为EF∥CD，
所以∠AEF就是异面直线AE与CD所成的角（或其补角）． …（2分）
在△AEF中，AE=AF=2
，EF=1，…（1分）
所以cos∠AEF=
=
． …（2分）
所以，异面直线AE与CD所成的角的大小为arccos
． …（1分）
（2）作AO⊥平面BCD，则O是正△BCD的中心，…（1分）
连结OE，OE=
，…（1分）
所以AO=
=
，…（1分）
所以，V=
•Sh=
×
×4×
=
． …（2分）
因为EF∥CD，
所以∠AEF就是异面直线AE与CD所成的角（或其补角）． …（2分）
在△AEF中，AE=AF=2
| 2 |
所以cos∠AEF=
| ||
2
|
| ||
| 8 |
所以，异面直线AE与CD所成的角的大小为arccos
| ||
| 8 |
（2）作AO⊥平面BCD，则O是正△BCD的中心，…（1分）
连结OE，OE=
| ||
| 3 |
所以AO=
| AE2-EO2 |
|
所以，V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
|
| ||
| 3 |
点评：本题主要考查异面直线所成角的大小的求法以及锥体的体积计算，要求熟练掌握相应的公式．
练习册系列答案
相关题目
若-1≤x≤1时，函数f（x）=ax+2a+1的值有正值也有负值，则a的取值范围是（ ）
A、a≥-
| ||
| B、a≤-1 | ||
C、-1＜a＜-
| ||
| D、以上都不对 |