题目内容
某酒厂制作了3种不同的精美卡片,每瓶酒酒盒随机装入一张卡片,集齐3种卡片可获奖,现购买该种酒5瓶,能获奖的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:其概率模型为古典概型.
解答:
解:假设卡片3种为A,B,C,
5个酒瓶卡片排列组合一共有35=243种,
其中,包含了3种不同卡片的有:
3X 1Y 1Z(即3种卡片3,1,1分布):C
×2×3=60种,
2X 2Y 1Z:类似共有:C
×3×C
=15×6=90种,
所以最终概率为:
=
;
故选D.
5个酒瓶卡片排列组合一共有35=243种,
其中,包含了3种不同卡片的有:
3X 1Y 1Z(即3种卡片3,1,1分布):C
3 5 |
2X 2Y 1Z:类似共有:C
1 5 |
2 4 |
所以最终概率为:
| 90+60 |
| 243 |
| 50 |
| 81 |
故选D.
点评:本题考查了古典概型概率的求法,属于基础题.

练习册系列答案
相关题目
已知复数Z=1-i,则
=( )
| Z2-2Z |
| Z-1 |
| A、2 | B、-2 | C、-2i | D、2i |
已知sin(θ+π)<0,cos(θ-π)>0,则θ是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
“猿用肺呼吸,猫用肺呼吸,象用肺呼吸,所以一切哺乳动物都用肺呼吸”.此推理方法是( )
| A、完全归纳推理 | B、归纳推理 |
| C、类比推理 | D、演绎推理 |
“|x-A|<
,且|y-A|<
”是“|x-y|<?”(x,y,A,?∈R)的( )
| ? |
| 2 |
| ? |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
扇形的面积为6cm2,半径为2cm,则扇形的圆心角是( )
| A、3 | ||
| B、3π | ||
C、
| ||
D、
|
已知集合A={x|x2-2x>0},B={x|-2<x<
},则( )
| 6 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )
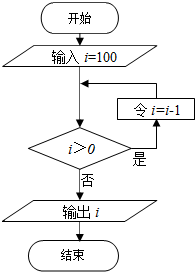

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |
已知定点M(x0,y0)在直线l:f(x,y)=0外,则方程f(x,y)=f(x0,y0)表示( )
| A、与l重合的直线 |
| B、与l平行的直线 |
| C、与l垂直的直线 |
| D、点M(x0,y0) |