题目内容
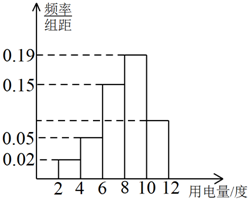 为了解某地区用电高峰期居民的用电量,抽取一个容量为200的样本,记录某天各户居民的用电量(单位:度),制成频率分布直方图,如图.
为了解某地区用电高峰期居民的用电量,抽取一个容量为200的样本,记录某天各户居民的用电量(单位:度),制成频率分布直方图,如图.(1)求样本数据落在区间[10,12]内的频数;
(2)若打算从[4,6)和[6,8)这两组中按分层抽样抽取4户居民作进一步了解,问各组分别抽取多少人?
(3)在(2)的基础上,为答谢上述4户居民的参与配合,从中再随机选取2户居民发放奖品,求这2户居民来不同组的概率是多少?
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)根据各组数据的累积频率为1,求出数据落在区间[10,12]的频率,再由频数=样本容量×频率得到答案;
(2)根据分层抽样对应成比例的性质,结合两组的频率之比,可求出两组抽取的户数;
(3)先计算从4号居民中随机选取2户居民的基本事件总数,和这2户居民来不同组的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)根据分层抽样对应成比例的性质,结合两组的频率之比,可求出两组抽取的户数;
(3)先计算从4号居民中随机选取2户居民的基本事件总数,和这2户居民来不同组的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)数据落在区间[10,12]的频率为:1-(0.02×2+0.05×2+0.15×2+0.19×2)=0.18…(2分)
数据落在区间[10,12]的频数为:200×0.18=36人.…(4分)
(2)数据落在区间[4,6)的频数为:200×0.05×2=20人;
数据落在区间[6,8)的频数为:200×0.15×2=60人.
二组频数之比为1:3,…(6分)
故:从用电量在区间[4,6)度中抽取的人数为:4×
=1人;…(7分)
从用电量在区间[6,8)度中抽取的人数为:4×
=3人;…(8分)
(3)记“这2户居民来自不同组”为事件A,
用电量在区间[6,8)度中的3人编号为:1、2、3
用电量在区间[4,6)度中的1人编号为:a…(9分)
则从4户居民中依次随机抽取2户的基本事件有:(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)共6种.…(10分)
事件B包含的基本事件有:(1,a),(2,a),(3,a),共3种.…(11分)
则P(B)=
=
.
所以从4户居民中随机抽取2户,抽到的2户居民来自不同组的概率为
.…(12分)
数据落在区间[10,12]的频数为:200×0.18=36人.…(4分)
(2)数据落在区间[4,6)的频数为:200×0.05×2=20人;
数据落在区间[6,8)的频数为:200×0.15×2=60人.
二组频数之比为1:3,…(6分)
故:从用电量在区间[4,6)度中抽取的人数为:4×
| 1 |
| 4 |
从用电量在区间[6,8)度中抽取的人数为:4×
| 3 |
| 4 |
(3)记“这2户居民来自不同组”为事件A,
用电量在区间[6,8)度中的3人编号为:1、2、3
用电量在区间[4,6)度中的1人编号为:a…(9分)
则从4户居民中依次随机抽取2户的基本事件有:(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)共6种.…(10分)
事件B包含的基本事件有:(1,a),(2,a),(3,a),共3种.…(11分)
则P(B)=
| 3 |
| 6 |
| 1 |
| 2 |
所以从4户居民中随机抽取2户,抽到的2户居民来自不同组的概率为
| 1 |
| 2 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若{an}是等比数列,其公比是q,且-a5,a4,a6成等差数列,则q等于( )
| A、1或2 |
| B、1或-2 |
| C、-1或 2 |
| D、-1或-2 |