题目内容
若△ABC的面积为2
，且b=2，A=60°，
（1）求c和a的值；
（2）求
的值．
| 3 |
（1）求c和a的值；
（2）求
| b |
| sinB |
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）先根据三角形的面积求得c的值，进而根据余弦定理求得a．
（2）由正弦定理直接求得
的值．
（2）由正弦定理直接求得
| b |
| sinB |
解答：
解：（1）∵S=
bcsinA=
•2•c•
=2
，
∴c=4．
a=
=
=2
．
（2）由正弦定理知
=
=
=4．
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴c=4．
a=
| b2+c2-2bccosA |
4+16-2×2×4×
|
| 3 |
（2）由正弦定理知
| b |
| sinB |
| a |
| sinA |
2
| ||||
|
点评：本题主要考查了正弦定理和余弦定理的应用．正弦定理和余弦定理时解决三角形边角问题的重要工具．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知数列{an}中，an=
，则S20=（ ）
| 1 |
| 4n2-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
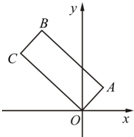如图，矩形OABC的顶点O为原点，AB边所在直线的方程为3x+4y-25=0，顶点B的纵坐标为10．
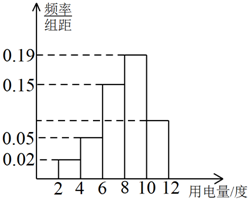为了解某地区用电高峰期居民的用电量，抽取一个容量为200的样本，记录某天各户居民的用电量（单位：度），制成频率分布直方图，如图．