题目内容
设函数f（x）=sinx+sin（x+
）．求f（x）的最小值，并求使f（x）取得最小值的x的集合．
| π |
| 3 |
考点：三角函数中的恒等变换应用
专题：常规题型,三角函数的图像与性质
分析：先利用两角和的正弦公式展开，然后逆用两角和的正弦公式化成正弦型函数的标准形式求最值．
解答：
解：f（x）=sinx+sin（x+
）
=sinx+sinxcos
+cosxsin
=
sinx+
cosx
=
sin（x+
）
∴当x+
=
+2kπ（k∈Z），即x=
+2kπ（k∈Z），
f（x）取最小值-
，
所以函数f（x）的最小值为-
，
此时x的集合{x|x=
+2kπ，（k∈Z）}．
| π |
| 3 |
=sinx+sinxcos
| π |
| 3 |
| π |
| 3 |
=
| 3 |
| 2 |
| ||
| 2 |
=
| 3 |
| π |
| 6 |
∴当x+
| π |
| 6 |
| 3π |
| 2 |
| 4π |
| 3 |
f（x）取最小值-
| 3 |
所以函数f（x）的最小值为-
| 3 |
此时x的集合{x|x=
| 4π |
| 3 |
点评：本题考查了两角和的正弦公式的运用及三角函数的最值，解题的关键是利用公式把函数化成正弦型函数的标准形式．
练习册系列答案
相关题目
为了得到函数y=sin3x+cos3x的图象，可以将函数y=
sin3x的图象（ ）
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
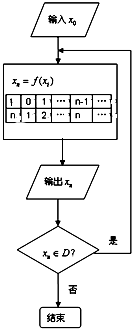对任意函数f（x），其定义域为D，可按如图所示，构造一个数列发生器，要求输入初始数据x0∈D，现定义f（x）=
