题目内容
一只口袋中装有形状、大小都相同的4只小球,其中2只红球,1只白球、1只黑球.
(1)若从中随机摸出1只球,求这只球为红球的概率;
(2)若从中一次随机摸出2只球,求这2只球颜色不同的概率.
(1)若从中随机摸出1只球,求这只球为红球的概率;
(2)若从中一次随机摸出2只球,求这2只球颜色不同的概率.
考点:相互独立事件的概率乘法公式,古典概型及其概率计算公式
专题:概率与统计
分析:(1)从4只小球摸出1只球共有4种结果,这4种结果是等可能的,记“从中随机摸出1只球,求这只球为红球”为事件A,事件A包含2种结果.由古典概型的概率公式求出概率
(2)从4只小球摸出2只球共有6种结果,这6种结果是等可能的,记“从中一次随机摸出2只球,求这2只球颜色不同”为事件B,她的对立事件
为两只球颜色相同,包含1种情况,由古典概型的概率公式求出概率
(2)从4只小球摸出2只球共有6种结果,这6种结果是等可能的,记“从中一次随机摸出2只球,求这2只球颜色不同”为事件B,她的对立事件
. |
| B |
解答:
解:(1)从4只小球摸出1只球共有4种结果,这4种结果是等可能的,记“从中随机摸出1只球,求这只球为红球”为事件A,
事件A包含2种结果,故P(A)=
=
(2)从4只小球摸出2只球共有6种结果,这6种结果是等可能的,
记“从中一次随机摸出2只球,求这2只球颜色不同”为事件B,她的对立事件
为两只球颜色相同,包含1种情况,
∴P(B)=1-
=
事件A包含2种结果,故P(A)=
| 2 |
| 4 |
| 1 |
| 2 |
(2)从4只小球摸出2只球共有6种结果,这6种结果是等可能的,
记“从中一次随机摸出2只球,求这2只球颜色不同”为事件B,她的对立事件
. |
| B |
∴P(B)=1-
| 1 |
| 6 |
| 5 |
| 6 |
点评:本题考查了独立事件的概率问题,求一个事件的概率时,应该先判断出事件的概率模型,然后选择合适的概率公式进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=x2+lnx的导数为( )
| A、f′(x)=2x+ex | ||
| B、f′(x)=2x+lnx | ||
C、f′(x)=2x+
| ||
D、f′(x)=2x-
|
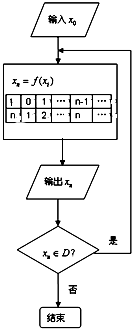 对任意函数f(x),其定义域为D,可按如图所示,构造一个数列发生器,要求输入初始数据x0∈D,现定义f(x)=
对任意函数f(x),其定义域为D,可按如图所示,构造一个数列发生器,要求输入初始数据x0∈D,现定义f(x)=
