题目内容
6.下列四个结论:①若x>0,则x>sinx恒成立;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”;
③“命题p∧q为真”是“命题p∨q为真”的充分不必要条件;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 构造函数,利用导数研究其单调性判断①;写出命题的逆否命题判断②;由复合命题的真假判断结合充分必要条件的判定方法判断③,写出全称命题的否定判断④.
解答 解:①令f(x)=x-sinx,则f′(x)=1-cosx≥0,
∴f(x)在(0,+∞)上为增函数,则x>0时,f(x)>f(0)=0,
∴若x>0,则x>sinx恒成立,故①正确;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”,故②正确;
③若命题p∧q为真,则p真且q真,∴命题p∨q为真;反之,若命题p∨q为真,则p真或q真,则命题p∧q不一定为真,
∴“命题p∧q为真”是“命题p∨q为真”的充分不必要条件,故③正确;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”,故④正确.
∴正确命题的个数是4个.
故选:D.
点评 本题考查命题的真假判断与应用,考查了复合命题的真假判断,考查充分必要条件的判定方法,训练了利用导数研究函数的单调性,是中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16.已知$\frac{\overline z}{1+2i}=2+i$,则复数z+5的实部与虚部的和为( )
| A. | 10 | B. | -10 | C. | 0 | D. | -5 |
14.已知集合A={-3,-2,-1},B={x|(x-1)(x+2)≤0,x∈Z},则A∪B=( )
| A. | {-1} | B. | {-2,-1} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1,0,1} |
1.若函数f(x)=(x-1)(x+2)(x2+ax+b)的图象关于直线x=0对称,则f(x)的最小值为( )
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
15.已知等比数列{an}的各项都为正数,且a3,$\frac{1}{2}{a_5},{a_4}$成等差数列,则$\frac{{{a_3}+{a_5}}}{{{a_4}+{a_6}}}$的值是( )
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
13.某人吃完饭后散步,在0到3小时内速度与时间的关系为v=t3-3t2+2t(km/h),这3小时内他走过的路程为( )
| A. | $\frac{9}{4}km$ | B. | $\frac{10}{4}km$ | C. | $\frac{11}{4}km$ | D. | $\frac{13}{4}km$ |
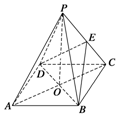 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.