题目内容
已知椭圆C1:
+
=1(b>0),抛物线C2:x2=4(y-b).过点F(0,b+1)作x轴的平行线,与抛物线C2在第一象限的交点为G,且该抛物线在点G处的切线经过坐标原点O.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设直线l:y=kx与椭圆C1相交于两点C、D两点,其中点C在第一象限,点A为椭圆C1的右顶点,求四边形ACFD面积的最大值及此时l的方程.
| x2 |
| 4b2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设直线l:y=kx与椭圆C1相交于两点C、D两点,其中点C在第一象限,点A为椭圆C1的右顶点,求四边形ACFD面积的最大值及此时l的方程.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由x2=4(y-b),可得y=
x2+b,与y=b+1联立可得G(2,b+1),利用导数的几何意义可得切线的斜率,进而点到过点G的切线方程为y=x+b-1,
把(0,0)代入可得b=1即可点到椭圆的方程.
(Ⅱ)依题意有k>0,设C(xC,kxC),把y=kx与椭圆方程联立可得xC=
,利用SAFCD=S△CFD+S△ACD=
|OF|×2xC+
|OA|×2kxC,及其基本不等式的性质即可得出.
| 1 |
| 4 |
把(0,0)代入可得b=1即可点到椭圆的方程.
(Ⅱ)依题意有k>0,设C(xC,kxC),把y=kx与椭圆方程联立可得xC=
| 2 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)由x2=4(y-b),可得y=
x2+b,当y=b+1,得x=±2,
∴G(2,b+1),
由y′=
x,
∴y′|x=2=1,
∴过点G的切线方程为y-(b+1)=x-2,即y=x+b-1,
把(0,0)代入可得b=1.
即椭圆的方程为
+y2=1.
(Ⅱ)依题意有k>0,设C(xC,kxC),
由
得xC=
,
∴SACFD=S△CFD+S△ACD=
|OF|×2xC+
|OA|×2kxC
=2(1+k)xC=
=4
(*),
令t=1+k,k=t-1,t∈(1,+∞),
∈(0,1),
则
=
=
≤
,
当且仅当t=
,k=
时,等号成立.
∴SACFD≤2
,
∴四边形ACFD面积的最大值为2
,l的方程为y=
x.
| 1 |
| 4 |
∴G(2,b+1),
由y′=
| 1 |
| 2 |
∴y′|x=2=1,
∴过点G的切线方程为y-(b+1)=x-2,即y=x+b-1,
把(0,0)代入可得b=1.
即椭圆的方程为
| x2 |
| 4 |
(Ⅱ)依题意有k>0,设C(xC,kxC),
由
|
| 2 | ||
|
∴SACFD=S△CFD+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
=2(1+k)xC=
| 4(1+k) | ||
|
|
令t=1+k,k=t-1,t∈(1,+∞),
| 1 |
| t |
则
| (1+k)2 |
| 1+4k2 |
| t2 |
| 1+4(t-1)2 |
| 1 | ||||
5(
|
| 5 |
| 4 |
当且仅当t=
| 5 |
| 4 |
| 1 |
| 4 |
∴SACFD≤2
| 5 |
∴四边形ACFD面积的最大值为2
| 5 |
| 1 |
| 4 |
点评:本题考查了椭圆与抛物线的标准方程及其性质、利用导数研究切线方程、直线与椭圆相交问题转化为方程联立可得交点坐标、基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列函数在[
,π]上是增函数的是( )
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=cos2x |
| D、y=sin2x |
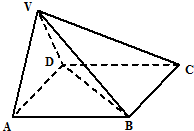 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.