题目内容

一几何体的三视图如图所示，若主视图和左视图都是等腰直角三角形，直角边长为1，则该几何体外接球的表面积为（　　）
A、4πB、3πC、2πD、π
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：根据三视图判断几何体为四棱锥，利用四棱锥补全正方体，即四棱锥的外接球即是边长为1的正方体的外接球，由此可得外接球的直径为
3
，代入球的表面积公式计算．
解答： 解：由主视图和左视图是腰长为1的两个全等的等腰直角三角形，得到这是一个四棱锥，
底面是一个边长是1的正方形，一条侧棱AE与底面垂直，可将此四棱锥放到一个棱长为1的正方体内，可知，此正方体与所研究的四棱锥有共同的外接球，
∴四棱锥的外接球即是边长为1的正方体的外接球，外接球的直径是AC
根据直角三角形的勾股定理知AC=
1+1+1
=
3
，

∴外接球的面积是4×π×（
3
2
）2=3π，
故选：B．
点评：本题考查由三视图求几何体外接球的表面积，解答此类问题的关键是根据数据所对应的几何量求得相关几何量的数据．
练习册系列答案
相关题目
已知一点A和平面a，求证：经过点A只能有一条直线和平面a垂直．
已知|
a
|=1，|
b
|=2，＜
a
，
b
＞=60°，则|
a
-2
b
|=
 
．
对于函数f（x）=a+
2
2x+1
x∈R是奇函数．
（1）求a值；
（2）用定义证明：f（x）在R上是单调减函数；
（3）解不等式f（2t+1）+f（t-5）≤0．
下列函数在[
π
2
，π]上是增函数的是（　　）
A、y=sinx
B、y=cosx
C、y=cos2x
D、y=sin2x
已知函数f（x）=ax3+bx-2，若f（2014）=10，则f（-2014）的值为
 
．
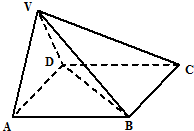在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．
（Ⅰ） 证明：AB⊥平面VAD；
（Ⅱ）求二面角A-VD-B的余弦值．
若O为坐标原点，点A在第三象限，且|OA|=4，∠xOA=210°，则
OA
坐标为
 
．
执行如图所示的程序框图，则输出的结果为（　　）
A、-2B、-1C、1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网