题目内容
已知圆C的圆心在坐标原点,且与直线l1:x-y-2
=0相切,点R(1,-1).
(Ⅰ)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N,求直线MN的方程;
(Ⅱ)若与直线l1垂直的直线l与圆C交于不同的两点P,Q,且∠PRQ为钝角,求直线l的纵截距的取值范围.
| 2 |
(Ⅰ)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N,求直线MN的方程;
(Ⅱ)若与直线l1垂直的直线l与圆C交于不同的两点P,Q,且∠PRQ为钝角,求直线l的纵截距的取值范围.
考点:圆的切线方程
专题:计算题,直线与圆
分析:(Ⅰ)设圆C的半径为r,运用直线和圆相切的条件:d=r,求得圆C的方程,再求以G点为圆心,线段GM长为半径的圆G方程,两方程相减即可得到MN的方程;
(Ⅱ)(方法一)设直线l的方程为:y=-x+b,联立圆C方程,运用判别式大于0,韦达定理以及向量的数量积的坐标表示,化简解不等式,即可得到所求范围;
(方法二)设直线l的方程为:y=-x+2m,取PQ中点M,则OM⊥PQ,点M坐标为M(m,m).若使∠PRQ为钝角,需满足点R在以PQ为直径的圆内,且点P,Q,R不共线,运用d<r,且三点共线知识,计算即可得到所求范围.
(Ⅱ)(方法一)设直线l的方程为:y=-x+b,联立圆C方程,运用判别式大于0,韦达定理以及向量的数量积的坐标表示,化简解不等式,即可得到所求范围;
(方法二)设直线l的方程为:y=-x+2m,取PQ中点M,则OM⊥PQ,点M坐标为M(m,m).若使∠PRQ为钝角,需满足点R在以PQ为直径的圆内,且点P,Q,R不共线,运用d<r,且三点共线知识,计算即可得到所求范围.
解答:
解:(Ⅰ)设圆C的半径为r,
由圆与直线l1:x-y-2
=0相切,
则r=
=2,
则圆C方程为x2+y2=4,
由点G(1,3),则|OG|=
=
,|GM|=
=
=
,
则以G点为圆心,线段GM长为半径的圆G方程(x-1)2+(y-3)2=6(1)
又圆C方程为::x2+y2=4(2)
由(1)-(2)得直线MN方程为x+3y-4=0;
(Ⅱ)(方法一)设直线l的方程为:y=-x+b,
联立x2+y2=4得:2x2-2bx+b2-4=0,
设直线l与圆的交点P(x1,y1),Q(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,
x1+x2=b,x1x2=
(3)
因为∠PRQ为钝角,所以
•
<0,
即满足(x1-1)(x2-1)+(y1+1)(y2+1)<0,
且
与
不是反向共线,又y1=-x1+b,y2=-x2+b,
所以(x1-1)(x2-1)+(y1+1)(y2+1)=2x1x2-(b+2)(x1+x2)+b2+2b+2<0(4)
由(3)(4)得b2<2,满足△>0,即-
<b<
,
当
与
反向共线时,直线y=-x+b过(1,-1),
此时b=0,不满足题意,
故直线l纵截距的取值范围是[-
,0)∪(0,
].
(方法二)设直线l的方程为:y=-x+2m,取PQ中点M,则OM⊥PQ,
点M坐标为M(m,m).
若使∠PRQ为钝角,需满足点R在以PQ为直径的圆内,且点P,Q,R不共线
即MR<
PQ即MR2<OP2-OM2即(m-1)2+(m+1)2<4-(m2+m2),
解得:m2<
,
当P,Q,R三点共线时,直线y=-x+2m过(1,-1),
此时m=0,不满足题意,所以2m∈[-
,0)∪(0,
].
故直线l纵截距的取值范围是[-
,0)∪(0,
].
由圆与直线l1:x-y-2
| 2 |
则r=
|0-0-2
| ||
|
则圆C方程为x2+y2=4,
由点G(1,3),则|OG|=
| 12+32 |
| 10 |
| OG2-OM2 |
| 10-4 |
| 6 |
则以G点为圆心,线段GM长为半径的圆G方程(x-1)2+(y-3)2=6(1)
又圆C方程为::x2+y2=4(2)
由(1)-(2)得直线MN方程为x+3y-4=0;
(Ⅱ)(方法一)设直线l的方程为:y=-x+b,
联立x2+y2=4得:2x2-2bx+b2-4=0,
设直线l与圆的交点P(x1,y1),Q(x2,y2),
由△=(-2b)2-8(b2-4)>0,得b2<8,
x1+x2=b,x1x2=
| b2-4 |
| 2 |
因为∠PRQ为钝角,所以
| RP |
| RQ |
即满足(x1-1)(x2-1)+(y1+1)(y2+1)<0,
且
| RP |
| RQ |
所以(x1-1)(x2-1)+(y1+1)(y2+1)=2x1x2-(b+2)(x1+x2)+b2+2b+2<0(4)
由(3)(4)得b2<2,满足△>0,即-
| 2 |
| 2 |
当
| RP |
| RQ |
此时b=0,不满足题意,
故直线l纵截距的取值范围是[-
| 2 |
| 2 |
(方法二)设直线l的方程为:y=-x+2m,取PQ中点M,则OM⊥PQ,
点M坐标为M(m,m).
若使∠PRQ为钝角,需满足点R在以PQ为直径的圆内,且点P,Q,R不共线
即MR<
| 1 |
| 2 |
解得:m2<
| 1 |
| 2 |
当P,Q,R三点共线时,直线y=-x+2m过(1,-1),
此时m=0,不满足题意,所以2m∈[-
| 2 |
| 2 |
故直线l纵截距的取值范围是[-
| 2 |
| 2 |
点评:本题考查直线和圆的位置关系,考查直线和圆相切的条件,同时考查两直线垂直的条件,运用向量的数量积小于0和构造圆的思想解决钝角问题是解题的关键.

练习册系列答案
相关题目
下列函数在[
,π]上是增函数的是( )
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=cos2x |
| D、y=sin2x |
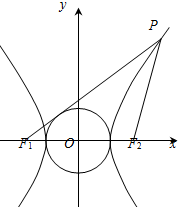 已知双曲线
已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x,y满足约束条件
,则z=3x+y的取值范围为( )
|
| A、[-1,1] |
| B、[-1,3] |
| C、[3,11] |
| D、[3,+∞) |
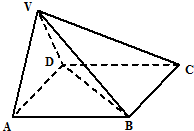 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.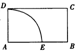 如图,四边形ABCD为矩形,AB=
如图,四边形ABCD为矩形,AB=