题目内容
已知函数f(x)=x2-1,则f(0)= ,f(-2)= .
考点:函数的值
专题:函数的性质及应用
分析:将x=0,-2代入函数解析式即可求出答案.
解答:
解:∵f(x)=x2-1,
∴f(0)=0-1=-1,
f(-2)=4-1=3,
故答案为:-1,3
∴f(0)=0-1=-1,
f(-2)=4-1=3,
故答案为:-1,3
点评:本题主要考查函数解析式,求函数值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
、
是平面α内的两个不相等的非零向量,非零向量
在直线l上,则
•
=0,且
•
=是l⊥α的( )
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知双曲线C1:
-
=1;C2:
-
=1,则双曲线C1,C2中的相同的量可以是( )
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| a2 |
| A、实轴长与顶点坐标 |
| B、渐近线方程与焦距 |
| C、离心率与渐近线方程 |
| D、对称轴与焦点坐标 |
已知非零向量
,
满足|
|=3|
|,且关于x的函数f(x)=
x3+
|
|x2+
•
x为R上增函数,则
,
夹角的取值范围是( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
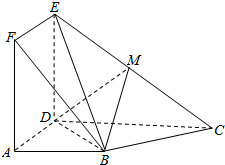 正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=