题目内容
在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2.
(Ⅰ)若C=
,且△ABC的面积等于
,求a,b;
(Ⅱ)若sinC+sin(B-A)=2sin2A,求a的取值范围.
(Ⅰ)若C=
| π |
| 3 |
| 3 |
(Ⅱ)若sinC+sin(B-A)=2sin2A,求a的取值范围.
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)由c与cosC的值,利用余弦定理列出关系式,利用三角形面积公式列出关系式,把sinC的值代入列出关系式,联立求出a,b的值即可;
(Ⅱ)已知等式右边利用二倍角的正弦函数公式化简,由cosA的值为0与不为0两种情况求出a的范围即可.
(Ⅱ)已知等式右边利用二倍角的正弦函数公式化简,由cosA的值为0与不为0两种情况求出a的范围即可.
解答:
解:(Ⅰ)∵c=2,C=
,∴由余弦定理得:a2+b2-ab=4,
又∵△ABC的面积等于
,
∴
absinC=
,即ab=4,
联立方程组
,
解得:a=b=2;
(Ⅱ)由题意得:sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,
当cosA=0,即A=
时,a2=b2+4>4,故a∈(2,+∞);
当cosA≠0,即A≠
时,得sinB=2sinA,由正弦定理得b=2a,
由三条边构成三角形的条件可得:
,即a∈(
,2),
综上:当A=
时,a∈(2,+∞);当A≠
时,a∈(
,2).
| π |
| 3 |
又∵△ABC的面积等于
| 3 |
∴
| 1 |
| 2 |
| 3 |
联立方程组
|
解得:a=b=2;
(Ⅱ)由题意得:sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,
当cosA=0,即A=
| π |
| 2 |
当cosA≠0,即A≠
| π |
| 2 |
由三条边构成三角形的条件可得:
|
| 2 |
| 3 |
综上:当A=
| π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
点评:此题考查了余弦定理,三角形面积公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
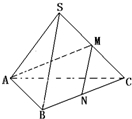 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
A、
| ||
| B、9π | ||
| C、12π | ||
| D、16π |
在锐角△ABC中,角A、B、C所对应的边分别为a,b,c,若b=2asinB,则角A等于( )
| A、30° | B、45° |
| C、60° | D、75° |
将函数h(x)=2sin(2x+
)的图象向右平移
个单位向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
| π |
| 4 |
| π |
| 4 |
| A、关于直线x=0对称 | ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于点(
|
设x,y都是正数,且2x+y=1,则
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
A、4
| ||
B、3
| ||
C、2+3
| ||
D、3+2
|