题目内容
复数z=m2(
+i)+(6m-16)i-
.(i为虚数单位)
(1)若复数z为纯虚数,求实数m的值;
(2)若复数z对应的点在第三象限或第四象限,求实数m的取值范围.
| 1 |
| m+8 |
| m+2 |
| m+8 |
(1)若复数z为纯虚数,求实数m的值;
(2)若复数z对应的点在第三象限或第四象限,求实数m的取值范围.
考点:复数的基本概念,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(1)复数z为纯虚数,复数的实部为0,虚部不为0,即可求实数m的值;
(2)若求出复数的对应点的坐标,通过复数z对应的点在第三象限或第四象限,求实数m的取值范围.
(2)若求出复数的对应点的坐标,通过复数z对应的点在第三象限或第四象限,求实数m的取值范围.
解答:
解:复数z=m2(
+i)+(6m-16)i-
.(1)若复数z为纯虚数,∴
,
解得:m=-1.
(2)复数z对应的点(
-
,m2+6m-16),
复数z对应的点在第三象限或第四象限,
∴
,
解得:m∈(-8,2)∪{-1}.
| 1 |
| m+8 |
| m+2 |
| m+8 |
|
解得:m=-1.
(2)复数z对应的点(
| m2 |
| m+8 |
| m+2 |
| m+8 |
复数z对应的点在第三象限或第四象限,
∴
|
解得:m∈(-8,2)∪{-1}.
点评:本题考查复数的基本概念的应用,注意复数是纯虚数时,复数的虚部不为0,考查基本知识的应用.

练习册系列答案
相关题目
20和16的等比中项是( )
| A、18 | ||||
| B、320 | ||||
C、8
| ||||
D、-8
|
i是虚数单位,若集合S={-2,0,1},则( )
| A、i2015∈S | ||
| B、-2i2014∈S | ||
| C、i2013∈S | ||
D、i(i-
|
 如图,在半径为4,圆心角为变量2θ(0<θ<2π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相内切并与圆P外切的小圆Q,记圆Q的半径为y.
如图,在半径为4,圆心角为变量2θ(0<θ<2π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相内切并与圆P外切的小圆Q,记圆Q的半径为y.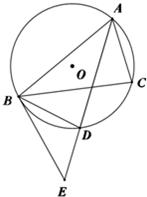 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.