题目内容
从装有3个白球,4个红球的箱子中,随机取出了3个球,恰好是2个白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:计算出从装有3个白球,4个红球的箱子中,随机取出了3个球的取法总数,及恰好是2个白球的取法个数,代入古典概型概率计算公式,可得答案.
解答:
解:从装有3个白球,4个红球的箱子中,随机取出了3个球,
共有
=35种不同的方法,
其中取出的3个球,恰好是2个白球,
共有
•
=12种方法,
故取出的3个球,恰好是2个白球的概率P=
,
故选:C
共有
| C | 3 7 |
其中取出的3个球,恰好是2个白球,
共有
| C | 2 3 |
| C | 1 4 |
故取出的3个球,恰好是2个白球的概率P=
| 12 |
| 35 |
故选:C
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
定积分
(
-x)dx等于( )
| ∫ | 1 0 |
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知等边三角形的边长为4,那么它水平放置的直观图的面积为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
已知
,
是夹角为60°的两个单位向量,则
=2
+
与
=-3
+2
的夹角的正弦值是( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
复数z=3-2i所对应的点位于复平面的( )
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
若a=0.63,b=log30.2,c=30.6,则( )
| A、c>a>b |
| B、a>c>b |
| C、c>b>a |
| D、b>c>a |
若抛物线y2=4x的焦点是F,准线是l,则经过点F、M(4,4)且与l相切的圆共有( )
| A、4个 | B、2个 | C、1个 | D、0个 |
若四点A(5,0),B(-1,0),C(a,2),D(3,-2)共圆,则正实数a=( )
| A、2 | B、3 | C、4 | D、5 |
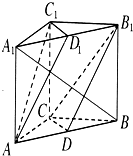 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.