题目内容
已知cosα=
，cos（α-β）=
，0＜β＜α＜
，求tan（α+2β）的值．
| 1 |
| 7 |
| 13 |
| 14 |
| π |
| 2 |
考点：两角和与差的正切函数,两角和与差的余弦函数
专题：三角函数的求值
分析：依题意，可求得sin（α-β）与sinα、tanα的值，继而得到tanβ与tan2β的值，利用两角和的正切即可求得tan（α+2β）．
解答：
解：∵0＜β＜α＜
，∴0＜α-β＜
，（3分）
又cos（α-β）=
，cosα=
，
∴sin（α-β）=
=
，sinα=
，tanα=4
；（6分）
∴sinβ=sin[α-（α-β）]=sinαcos（α-β）-cosαsin（α-β）=
； （8分）
∴cosβ=
，tanβ=
，tan2β=
=-
．（11分）
∴tan（α+2β）=
=
=
．（12分）
| π |
| 2 |
| π |
| 2 |
又cos（α-β）=
| 13 |
| 14 |
| 1 |
| 7 |
∴sin（α-β）=
| 1-cos2(α-β) |
3
| ||
| 14 |
4
| ||
| 7 |
| 3 |
∴sinβ=sin[α-（α-β）]=sinαcos（α-β）-cosαsin（α-β）=
| ||
| 2 |
∴cosβ=
| 1 |
| 2 |
| 3 |
| 2tanβ |
| 1-tan2β |
| 3 |
∴tan（α+2β）=
| tanα+tan2β |
| 1-tanαtan2β |
4
| ||||
1-4
|
3
| ||
| 13 |
点评：本题考查两角和与差的正弦与正切，考查同角三角函数间的关系式的应用，属于中档题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图是函数y=f（x）的导函数的图象，则正确的判断是（ ）
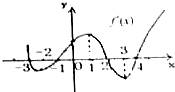
| A、f（x）在（-2，1）上是增函数 |
| B、x=1是f（x）的极大值点 |
| C、f（x）在（-1，2）上是增函数，在（2，4）上是减函数 |
| D、x=3是f（x）的极小值点 |